Конфігурація Дезарга

Конфігурація Дезарга — конфігурація десяти точок і десяти прямих, у якій кожна пряма містить три точки конфігурації, і через будь-яку точку проходять три прямих. Конфігурацію названо на честь Жерара Дезарга і вона тісно пов'язана з теоремою Дезарга, яка доводить існування таких конфігурацій.

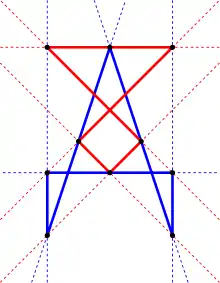
Конфігурація Дезарга у вигляді пари взаємно вписаних п'ятикутників: кожна вершина п'ятикутника лежить на прямій, що проходить через одну зі сторін іншого п'ятикутника.

Побудови

Двовимірний простір
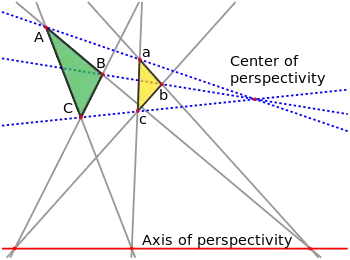
Два трикутники в перспективі, їх центр і вісь перспективи

Кажуть, що два трикутники ABC і abc перебувають у центральній перспективі, якщо прямі Aa, Bb і Cc перетинаються в одній точці (так званому центрі перспективи). Вони перебувають в осьовій перспективі, якщо точки перетину прямих, що проходять через відповідні сторони трикутників X = AB•ab Y = AC•ac і Z = BC•bc, лежать на одній прямій, на осі перспективи. Теорема Дезарга стверджує, що ці дві умови еквівалентні — якщо два трикутники перебувають у центральній перспективі, то вони повинні перебувати і в осьовій перспективі, і навпаки. У цьому випадку десять точок і десять прямих цих двох перспектив (шість вершин трикутників, три точки перетину на осі перспективи і центр перспективи, шість сторін трикутників, три прямих через центр перспективи і вісь перспективи) разом утворюють конфігурацію Дезарга.

Тривимірний простір

Хоча конфігурацію можна вкласти в площину, вона має дуже просту побудову в тривимірному просторі — будь-які п'ять площин у загальному положенні в евклідовому просторі, мають десять точок перетину трьох площин і десять прямих перетину двох площин і утворюють конфігурацію Дезарга[1]. Ця побудова тісно пов'язана зі властивістю, що будь-яка проєктивна площина, яку можна вкласти в проєктивний простір, підпорядковується теоремі Дезарга. Таке тривимірне подання конфігурації Дезарга називають також повним п'ятигранником[1].

Чотиривимірний простір

Пятикомірник або п'ятигранник (правильний симплекс у чотиривимірному просторі) має п'ять вершин, десять ребер, десять трикутних двовимірних граней і п'ять тетраедальних граней. Ребра і двовимірні грані перетинаються так само, як і точки з прямими в конфігурації Дезарга. Продовжимо ребра п'ятикомірника прямими і кожен трикутник до площини. Розглянемо перетин цих прямих і площин із тривимірною гіперплощиною, яка не містить цих прямих і площин, а також не паралельна їм. Кожна пряма перетинає гіперплощину в точці, а кожна площина перетинає гіперплощину по прямій. Ці десять точок і прямих утворюють конфігурацію Дезарга[1].

Симетрії

Хоча в теоремі Дезарга точки і прямі відіграю́ть різні ролі, конфігурація Дезарга симетричніша — будь-яку з десяти точок можна обрати центром перспективи, і цей вибір визначає, які шість точок будуть вершинами трикутників і яка пряма буде віссю перспективи. Конфігурація Дезарга має групу симетрії порядку 120. Отже, є 120 різних способів перестановки точок і прямих у конфігурації, що зберігають інцидентність точки і прямої. Тривимірне подання конфігурації Дезарга робить ці симетрії більш явними — якщо конфігурацію отримано з п'яти площин у тривимірному просторі в загальному положенні, то кожна зі 120 різних перестановок цих п'яти площин відповідає симетрії в конфігурації Дезарга[1].

Конфігурація Дезарга самодвоїста, що означає, що можна знайти відповідність точок першої конфігурації прямим у другій конфігурації і прямих першої точкам другої таким способом, що всі інцидентності збережуться[2].

Графи

Граф Леві конфігурації Дезарга, що має по одній вершині для кожної точки і по одній вершині для кожної прямої в конфігурації, відомий як граф Дезарга. Зважаючи на симетрії та самодвоїстість конфігурації Дезарга граф Дезарга є симетричним графом.

Граф Петерсена в поданні, запропонованому Кемпе (Kempe, 1886)

Кемпе запропонував для цієї конфігурації інший граф, що має десять вершин, відповідних прямим, і ребра, що з'єднують дві вершини, якщо точка перетину двох прямих не належить конфігурації. Можна інтерпретувати цей граф іншим способом — вершини графу відповідають точкам конфігурації Дезарга, а ребра в цьому випадку відповідають прямим, якщо пряма, що проходить через ці точки, не належить конфігурації. Ця публікація є першим відомим джерелом у математичній літературі, в якому з'явився граф Петерсена, за 12 років до того, як Юліус Петерсен використав той самий граф як контрприклад у задачі реберного розфарбовування.

Пов'язані конфігурації
Конфігурація (103103), що не є дезарговою

Як проєктивна конфігурація, конфігурація Дезарга має позначення (103103), що означає, що кожна з її 10 точок інцидентна трьом прямим, а кожна з 10 прямих інцидентна трьом точкам. Її десять точок можна розглядати єдиним способом як два взаємно вписаних п'ятикутники або як вписаний в самого себе десятикутник[3]. Граф Дезарга, двочастковий симетричний кубічний граф з 20 вершинами, названо цим ім'ям, оскільки його можна подати як граф Леві конфігурації Дезарга, з вершиною для кожної точки і для кожної прямої і ребром для кожної інциденції точка-пряма.

Існує ще вісім інших (103103) конфігурацій (тобто множин точок і прямих в евклідовій площині, в яких будь-яка точка лежить на трьох прямих і будь-яка пряма містить три точки), які не ізоморфні відносно відношення інцидентності конфігурації Дезарга, і одну з цих конфігурацій показано на малюнку. У всіх цих конфігураціях для будь-якої вибраної точки завжди існують три інших, що не лежать з нею на одній прямій і ці точки не лежать на одній прямій. У конфігурації ж Дезарга ці три точки завжди лежать на одній прямій. Так, якщо виберемо центр перспективи, то ці три точки лежать на осі перспективи. На прикладі ж, наведеному на малюнку, такі точки формують трикутник. Як і у випадку конфігурації Дезарга, інші конфігурації можна подати у вигляді пари взаємно вписаних один в одного п'ятикутників.

Див. також

Примітки
  1. Barnes, 2012.
  2. Coxeter, 1964.
  3. Hilbert, Cohn-Vossen, 1952.

Література
  • Barnes John. Gems of Geometry. — Springer, 2012. — С. 95–97. — ISBN 9783642309649.
  • H.S.M Coxeter. Projective Geometry. — New York : Blaisdell, 1964. — С. 26–27.
  • David Hilbert; Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — Chelsea, 1952. — С. 119–128. — ISBN 0-8284-1087-9.
  • A. B. Kempe. A memoir on the theory of mathematical form // Philosophical Transactions of the Royal Society of London. — 1886. — Т. 177 (17 лютого). — С. 1–70. — DOI:10.1098/rstl.1886.0002.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.