Симетричний граф
В теорії графів, граф G є симетричним (або дуго-транзитивним) якщо, для будь-яких пар суміжних вершин u1—v1 і u2—v2 графу G, існує автоморфізм
- f : V(G) → V(G)
такий, що
- f(u1) = u2 and f(v1) = v2.[1]
Інакше кажучи, граф симетричний, якщо група його автоморфізмів діє транзитивно над впорядкованими парами суміжних вершин (тобто, над орієнтованими ребрами).[2] Такий граф іноді називають 1-дуго-транзитивний[2] або прапорцево-транзитивний.[3]
За визначенням (ігноруючи u1 і u2), симетричний граф без ізольованих вершин має також бути вершинно-транзитивним.[1] Завдяки визначенню через відображення одного ребра на інше, симетричний граф має також бути реберно-транзитивним. Однак, реберно-транзитивний граф не має бути симетричним, бо a—b можуть відбиватись в c—d, але не в d—c. Наприклад, напівсиметричний граф є реберно-транзитивним і регулярним, але не вершинно-транзитивним.
| Види графів за їхніми автоморфізмами | ||||
| відстанево-транзитивний | відстанево-регулярний | сильно регулярний | ||
| симетричний (дуго-транзитивний) | t-транзитивний, t ≥ 2 | |||
| (якщо зв'язний) | ||||
| вершинно- та реберно-транзитивний | реберно-транзитивний і регулярний | реберно-транзитивний | ||
| вершинно-транзитивний | регулярний | |||
| граф Келі | кососиметричний | асиметричний | ||
Таким чином, кожний зв'язний симетричний граф має бути і вершинно-транзитивним, і реберно-транзитивним, зворотне твердження теж правильне для графів непарних степенів.[3] Однак, для парних степенів, існують зв'язні вершинно-транзитивні і реберно-транзитивні, але не симетричні графи.[4] Такі графи називаються напівтранзитивними.[5] Найменший зв'язний напівтранзитивний граф це граф Хольта, зі степенем 4 і 27 вершинами.[1][6] Деякі автори використовують термін «симетричний граф» для позначення графів, що вершинно-транзитивні і реберно-транзитивні, радше ніж дуго-транзитивні. Таке визначення охоплює напівтранзитивні графи, які виключені визначенням поданим вище.
У відстанево-транзитивного графу замість розглядання пар суміжних вершин (тобто вершин на відстані 1), визначення розглядає дві пари вершин, кожна з однаковою відстанню між вершинами. Такий граф автоматично симетричний за визначенням.[1]
Визначимо t-дугу як послідовність з t+1 вершин таких, що будь-які дві послідовні вершини суміжні, з допустимою відстанню між вершинами, що повторюються, більшою за два кроки. T-транзитивний граф це такий граф, що група автоморфізмів діє транзитивно на t-дугах, але не на (t+1)-дугах. Через те, що 1-дуги це просто ребра, кожний симетричний граф степені 3 або більше має бути t-транзитивний для деякого t, і значення t можна використати для подальшої класифікації симетричних графів. Куб є 2-транзитивним, наприклад.[1]
Приклади
Поєднання умови симетричності з накладанням обмеження кубічності на граф (тобто всі вершини мають степінь 3) породжує дуже сильну умову, і такі графи становляться досить рідкісними, щоб бути занесеними в список. Перепис Фостера (англ. Foster census) і його розширення подають такі списки.[7] Перепис Фостера був початий в 1930 році Рональдом Фостером коли він працював у Bell Labs,[8] і в 1988 (коли Фостеру було 92[1]) складений на той момент його перелік (список всіх кубічних симетричних графів до 512 вершин) був опублікованим у формі книги.[9] Перші тринадцять елементів цього списку це кубічні симетричні графи до 30 вершин[10][11] (десять з них також відстанево-транзитивні; винятки позначені):
| Вершин | Діаметр | Обхват | Граф | Примітки |
|---|---|---|---|---|
| 4 | 1 | 3 | Повний граф K4 | відстанево-транзитивний, 2-transitive |
| 6 | 2 | 4 | Повний дводольний граф K3,3 | відстанево-транзитивний, 3-транзитивний |
| 8 | 3 | 4 | Вершини і ребра куба | відстанево-транзитивний, 2-транзитивний |
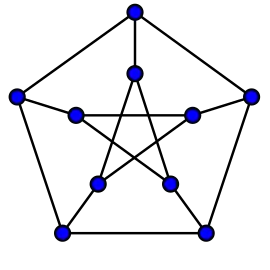
| 10 | 2 | 5 | Граф Петерсена | відстанево-транзитивний, 3-транзитивний |
| 14 | 3 | 6 | Граф Хівуда | відстанево-транзитивний, 4-транзитивний |
| 16 | 4 | 6 | Граф Мебіуса — Кантора | 2-транзитивний |
| 18 | 4 | 6 | Граф Паппуса | відстанево-транзитивний, 3-транзитивний |
| 20 | 5 | 5 | Вершини і ребра додекаедра | відстанево-транзитивний, 2-транзитивний |
| 20 | 5 | 6 | Граф Дезарга | відстанево-транзитивний, 3-транзитивний |
| 24 | 4 | 6 | Граф Науру (узагальнений граф Петерсена G(12,5)) | 2-транзитивний |
| 26 | 5 | 6 | Граф F26A[11] | 1-транзитивний |
| 28 | 4 | 7 | Граф Коксетера | відстанево-транзитивний, 3-транзитивний |
| 30 | 4 | 8 | Граф Тютте-Коксетера | відстанево-транзитивний, 5-транзитивний |
Іншими добре відомими кубічними симетричними графами є граф Діка, граф Фостера і граф Біґґса–Сміта. Десять відстанево-транзитивних графів, які перелічені вище, разом із графом Фостера і графом Біґґса—Сміта, є єдиними кубічними відстанево-транзитивними графами.
Некубічні симетричні графи включають циклічні графи (степеня 2), повні графи (степеня 4 або вище, коли вони мають 5 або більше вершин), графи гіперкуби (степеня 4 або вище, коли вони мають 16 або більше вершин), і графи утворені вершинами і ребрами октаедра, ікосаедра, кубооктаедра та ікосододекаедра. Граф Редо створює приклад симетричного графу з нескінченною кількістю вершин і нескінченним степенем.
Примітки
- Biggs, Norman (1993). Algebraic Graph Theory (вид. 2nd). Cambridge: Cambridge University Press. с. 118–140. ISBN 0-521-45897-8.
- Godsil, Chris; Royle, Gordon (2001). Algebraic Graph Theory. New York: Springer. с. 59. ISBN 0-387-95220-9.
- Babai, L (1996). Automorphism groups, isomorphism, reconstruction. У Graham, R; Groetschel, M; Lovasz, L. Handbook of Combinatorics. Elsevier.
- Bouwer, Z. «Vertex and Edge Transitive, But Not 1-Transitive Graphs.» Canad. Math. Bull. 13, 231—237, 1970.
- Gross, J.L. and Yellen, J. (2004). Handbook of Graph Theory. CRC Press. с. 491. ISBN 1584880902.
- Holt, Derek F. (1981). A graph which is edge transitive but not arc transitive. Journal of Graph Theory 5 (2): 201–204. doi:10.1002/jgt.3190050210..
- Marston Conder, Trivalent symmetric graphs on up to 768 vertices, J. Combin. Math. Combin. Comput, vol. 20, pp. 41—63
- Foster, R. M. «Geometrical Circuits of Electrical Networks.» Transactions of the American Institute of Electrical Engineers 51, 309—317, 1932.
- «The Foster Census: R.M. Foster's Census of Connected Symmetric Trivalent Graphs», by Ronald M. Foster, I.Z. Bouwer, W.W. Chernoff, B. Monson and Z. Star (1988) ISBN 0-919611-19-2
- Biggs, p. 148
- Weisstein, Eric W., «Cubic Symmetric Graph», from Wolfram MathWorld.
