Критерій абсолютної стійкості В.М.Попова

Критерій абсолютної стійкості В. М. Попова — для встановлення абсолютної стійкості нелінійної системи досить підібрати таку пряму на комплексній площині W*(jω), що проходить через точку (1/k, j0), щоб вся крива W*(jω) лежала праворуч від цієї прямої — тобто щоб пряма проведена через точку (1/k, j0) не перетинала годограф амплідудно-фазової частотної характеристики (АФЧХ). Умови виконання теореми показані на рис.

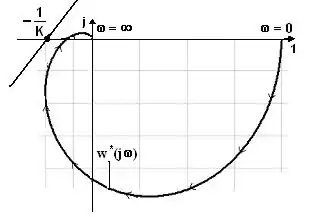
Критерій абсолютної стійкості В. М. Попова. Випадок стійкої системи.

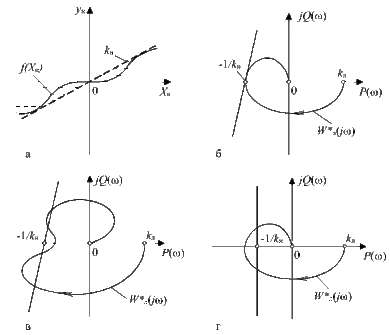
Критерій абсолютної стійкості В. М. Попова. а — до визначення коефіцієнта k, б — система на грані стійкості, в, г — нестійкі системи.

Якщо таку пряму провести не можна, то це означає, що абсолютна стійкість для даної системи неможлива. Обрис нелінійності може бути невідомим. Критерій доцільно застосовувати у випадках, коли нелінійність може в процесі роботи САУ змінюватися, або її математичний опис невідомо.