Лінійна динамічна система

У лінійній динамічній системі, зміна вектора стану (${\displaystyle N}$-вимірний вектор позначуваний ${\displaystyle \mathbf {x} }$) дорівнює сталій матриці (позначуваній ${\displaystyle \mathbf {A} }$) помноженій на ${\displaystyle \mathbf {x} }$. Ця варіація може набувати дві форми: або як потік, в якому ${\displaystyle \mathbf {x} }$ змінюється неперервно з часом

${\displaystyle {\frac {d}{dt}}\mathbf {x} (t)=\mathbf {A} \cdot \mathbf {x} (t)}$

або як відображення, в якому ${\displaystyle \mathbf {x} }$ змінюється дискретними кроками

${\displaystyle \mathbf {x} _{m+1}=\mathbf {A} \cdot \mathbf {x} _{m}}$

Ці рівняння є лінійними у сенсі: якщо ${\displaystyle \mathbf {x} (t)}$ і ${\displaystyle \mathbf {y} (t)}$ є двома розв'язками, тоді будь-яка їхня лінійна комбінація, наприклад, ${\displaystyle \mathbf {z} (t)\ {\stackrel {\mathrm {def} }{=}}\ \alpha \mathbf {x} (t)+\beta \mathbf {y} (t)}$ де ${\displaystyle \alpha }$ і ${\displaystyle \beta }$ є довільними скалярами. Матриця ${\displaystyle \mathbf {A} }$ може не бути симетричною.

Лінійну динамічну систему можна розв'язати точно, на відміну від більшості нелінійних. Іноді, нелінійні системи також можна розв'язати точно через перехід до лінійної системи. Більше, розв'язки (майже) будь-якої нелінійної системи можна добре наблизити тотожними лінійними системами біля її нерухомих точок. Отже, розуміння лінійних систем і їхніх розв'язків є важливим кроком для розуміння складніших нелінійних систем.

Якщо початковий вектор ${\displaystyle \mathbf {x} _{0}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {x} (t=0)}$ колінеарний з правим власним вектором ${\displaystyle \mathbf {r} _{k}}$ матриці ${\displaystyle \mathbf {A} }$, тоді динаміка проста

${\displaystyle {\frac {d}{dt}}\mathbf {x} (t)=\mathbf {A} \cdot \mathbf {r} _{k}=\lambda _{k}\mathbf {r} _{k}}$

де ${\displaystyle \lambda _{k}}$ — це відповідне власне значення; розв'язком цього рівняння є

${\displaystyle \mathbf {x} (t)=\mathbf {r} _{k}e^{\lambda _{k}t}}$

що можна підтвердити підстановкою.

Якщо ${\displaystyle \mathbf {A} }$ є діагоналізовною, тоді будь-який вектор з ${\displaystyle N}$-вимірного простору можна представити як лінійну комбінацію правих і лівих власних векторів (позначуваних ${\displaystyle \mathbf {l} _{k}}$) матриці ${\displaystyle \mathbf {A} }$.

${\displaystyle \mathbf {x} _{0}=\sum _{k=1}^{N}\left(\mathbf {l} _{k}\cdot \mathbf {x} _{0}\right)\mathbf {r} _{k}}$

З цього, загальним розв'язком для ${\displaystyle \mathbf {x} (t)}$ є лінійна комбінація індивідуальних розв'язків для правих власних векторів

${\displaystyle \mathbf {x} (t)=\sum _{k=1}^{n}\left(\mathbf {l} _{k}\cdot \mathbf {x} _{0}\right)\mathbf {r} _{k}e^{\lambda _{k}t}}$

Подібні міркування застосовні і до дискретного відображення.

Лінійне наближення нелінійної системи: класифікація 2D нерухомої точки відповідно до сліду і визначника Якобіана (лінеаризація системи поблизу нерухомої точки).

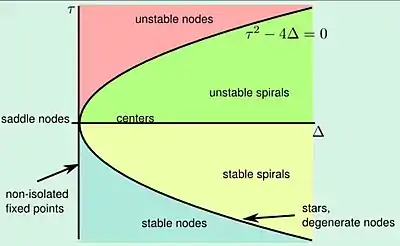
Корені характеристичного многочлена det(A - λI) є власними значеннями A. Знаки і зв'язок між цими коренями, ${\displaystyle \lambda _{n}}$, можна використати, щоб визначити стабільність динамічної системи.

${\displaystyle {\frac {d}{dt}}\mathbf {x} (t)=\mathbf {A} \mathbf {x} (t).}$

Для 2-вимірної системи, характеристичний многочлен має вигляд ${\displaystyle \lambda ^{2}-\tau \lambda +\Delta =0}$ де ${\displaystyle \tau }$ є слідом і ${\displaystyle \Delta }$ є визначником A. Таким чином, маємо два корені такої форми:

${\displaystyle \lambda _{1}={\frac {\tau +{\sqrt {\tau ^{2}-4\Delta }}}{2}}}$

${\displaystyle \lambda _{2}={\frac {\tau -{\sqrt {\tau ^{2}-4\Delta }}}{2}}}$

Зауважимо також, що ${\displaystyle \Delta =\lambda _{1}\lambda _{2}}$ і ${\displaystyle \tau =\lambda _{1}+\lambda _{2}}$. Отже, якщо ${\displaystyle \Delta <0}$ тоді власні значення мають протилежні знаки і нерухома точка є сідловою. Якщо ${\displaystyle \Delta >0,}$ тоді власні значення мають однаковий знак. З цього випливає, що якщо ${\displaystyle \tau >0}$ обидва додатні і точка нестабільна, і якщо ${\displaystyle \tau <0}$ тоді вони негативні і точка стабільна. Визначник показує перебуває точка у спіралі чи вузлі (тобто власні значення дійсні чи комплексні).

• Лінійна система
• Динамічна система