Лінійне рівняння

Лінійне рівняння — рівняння, обидві частини якого визначаються лінійними функціями. Найпростіший випадок має вигляд

a\cdot x=b

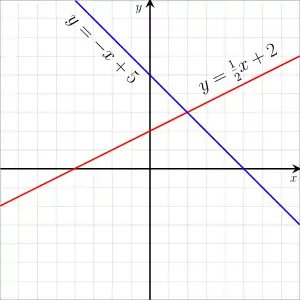
Графічне зображення лінійних рівнянь.

Числа а і b є коефіцієнтами лінійного рівняння: а — коефіцієнт при змінній, b — вільний член.

Отримали назву лінійних через те, що визначають лінію на площині або в просторі.

У загальному випадку лінійним рівнянням є рівняння, що має наступну форму:

a_{1}x_{1}+\cdots +a_{n}x_{n}+b=0,

де $x_{1},\ldots ,x_{n}$ — змінні (невідомі або невизначені) рівняння, а $b,a_{1},\ldots ,a_{n}$ — коефіцієнти, що як правило є дійсними числами. Коефіцієнти можна розглядати як параметри рівняння, і можуть задаватися як довільні вирази, які не повинні мати ніяких змінних.

Розв'язком такого рівняння будуть такі значення, які можна підставити замість невідомих, так що рівність стане істиною.

Властивості лінійних рівнянь

Якщо $a\neq 0$ , рівняння має єдиний розв'язок:

x={\frac {b}{a}}

Якщо тільки $a=0$ , рівняння не має жодного кореня:

x\cdot 0=b

Якщо ж і $a=0$ і $b=0$ , рівняння має безліч коренів:

x\cdot 0=0

Спрощення рівняння до лінійного

Виконувати в такій послідовності:

Позбутися знаменників, якщо вони є.
Розділити рівняння на лінійні, якщо його подано у вигляді рівного нулеві добутку сум.
Розкрити дужки, якщо вони є. Якщо після цього утворилося багато членів у будь-якій його частині, то доцільно спочатку звести подібні доданки, а потім виконувати переноси.
Перенести члени зі змінними в ліву частину, а числа — в праву.
Звести подібні доданки.
Знайти корені.

Див. також

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.