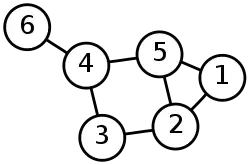
Матриця Кірхгофа

Дано простий граф${\displaystyle \ G}$ з ${\displaystyle \ |V(G)|=n}$ вершинами. Тоді матриця Кірхгофа ${\displaystyle \ K=(k_{i,j})_{n\times n}}$ цього графу буде визначатися так:

${\displaystyle \ k_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\-1&{\mbox{if}}\ (v_{i},v_{j})\in E(G),\\0&{\mbox{otherwise}}.\end{cases}}}$

Також матрицю Кірхгофа можна визначити як різницю матриць ${\displaystyle \ K=D-A,}$ де ${\displaystyle \ A}$ — це матриця суміжності цього графу, а ${\displaystyle \ D=(d_{i,j})_{n\times n}}$ — матриця, на головній діагоналі якої степені вершин графу, а решта елементів — нулі:

${\displaystyle \ d_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}$

Якщо граф є зваженим, то визначення матриці Кірхгофа узагальнюється. У цьому випадку елементами головної діагоналі матриці Кірхгофа будуть суми ваг ребер, інцидентних відповідній вершині. Для суміжних (пов'язаних) вершин ${\displaystyle \ k_{i,j}=-c(v_{i},v_{j})}$, де ${\displaystyle \ c(v_{i},v_{j})}$ — це вага (провідність) ребра. Для різних не суміжних (не пов'язаних) вершин покладається ${\displaystyle \ k_{i,j}=0}$.

${\displaystyle \ k_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\-c(v_{i},v_{j})&{\mbox{if}}\ (v_{i},v_{j})\in E(G),\\0&{\mbox{otherwise}}.\end{cases}}}$

Для зваженого графу матриця суміжності ${\displaystyle \ A}$ записується з урахуванням провідностей ребер, а на головній діагоналі матриці ${\displaystyle \ D}$ будуть суми провідностей ребер, інцидентних відповідним вершинам.

${\displaystyle \ d_{i,j}:={\begin{cases}\sum _{\begin{smallmatrix}u\in V(G)\\(v_{i},u)\in E(G)\end{smallmatrix}}^{}c(v_{i},u)&{\mbox{if}}\ i=j,\\0&{\mbox{otherwise}}.\end{cases}}}$

Приклад матриці Кірхгофа простого графу.

Розмічений граф	Матриця Кірхгофа
	${\displaystyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

• Сума елементів кожного рядка (стовпця) матриці Кірхгофа дорівнює нулю:

  ${\displaystyle \ \sum _{i=1}^{|V(G)|}k_{i,j}=0}$.

• Визначник матриці Кірхгофа дорівнює нулю:

  ${\displaystyle \det K=0}$

• Матриця Кірхгофа простого графу симетрична:

  ${\displaystyle \ k_{i,j}=k_{j,i}\quad i,j=1,\ldots ,|V(G)|}$.

• Всі алгебраїчні доповнення ${\displaystyle \ K_{(ij)}}$ симетричної матриці Кірхгофа рівні між собою — стала матриці Кірхгофа. Для простого графу значення цієї сталої збігається з числом всіх можливих кістяків графу.

• Якщо зважений граф являє собою електричну мережу, де вага кожного ребра відповідає його провідності, то мінори матриці Кірхгофа дозволяють обчислити резистивні відстані (resistance distance) ${\displaystyle \ R_{ij}}$ між точками ${\displaystyle \ i}$ і ${\displaystyle \ j}$ даної мережі:

  ${\displaystyle \ R_{ij}={\frac {K^{(i,j)}}{K_{(ij)}}}}$,

тут ${\displaystyle \ K_{(ij)}}$ — стала (алгебраїчне доповнення) матриці Кірхгофа, а ${\displaystyle \ K^{(i,j)}}$ — алгебраїчне доповнення 2-го порядку, тобто визначник матриці, отримуваної з матриці Кірхгофа викреслюванням двох рядків і двох стовпців${\displaystyle \ i,j}$.

• Існує алгоритм відновлення матриці Кірхгофа за матрицею опорів ${\displaystyle R_{ij}}$.
  • 0 є власним значенням матриці (відповідний власний вектор — всі одиниці), кратність його дорівнює числу зв'язних компонент графу.
  • Інші власні значення додатні. Друге за малістю значення Мирослав Фідлер назвав індексом зв'язності графу, відповідний власний вектор — вектор Фідлера.

• Матриця суміжності
• Степенева матриця
• Матриця інцидентності
• Дискретна математика