Метод Ліля

Метод запропонував австрійський інженер Едуард Ліль у 1867 році[1] і узагальнив у своїй пізнішій роботі.[2]

• 
  Розв'язання рівняння 2x⁵ + 4x⁴ + 4x³ + 3x² + 1,5 x + 0,75 = 0.
• 
  Не розв'язання рівняння 2x⁵ + 4x⁴ + 4x³ + 3x² + 1,5 x + 0,75 = 0.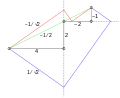
• 
  Три корені -1/2, -1/√2, 1/√2 многочлена 4х³ + 2х² − 2х − 1. Корені відповідають трьом уписаним прямокутним ламаним.

Від початку координат креслиться прямокутна ламана лінія. Перша ланка креслиться вправо, її довжина дорівнює старшому коефіцієнту; якщо він від'ємний, то ланка закінчується зліва від початку координат. Від кінця першої ланки наступна ланка креслиться вгору на величину другого коефіцієнта, потім наліво на величину третього, вниз на величину четвертого, і так далі. Послідовність напрямків змінюється циклічно вправо, вгору, вліво, вниз, потім повторюється. Таким чином, кожен поворот відбувається проти годинникової стрілки (якщо коефіцієнти додатні). Процес триває для кожного коефіцієнта полінома, включно з нулями. Для многочлена n-го степеня отримуємо ламану з n + 1 ланки.

В отриману ламану вписується прямокутна ламана, що з'єднує кінці початкової, з вершинами, розташованими послідовно на продовженнях ланок початкової ламаної. Кутовий коефіцієнт вписаної ламаної, взятий з оберненим знаком, є коренем початкового многочлена. Більш того, таким способом можна отримати будь-який дійсний корінь.

• У 1936 році Маргарита Белох використала метод Ліля під час розв'язування кубічних рівнянь за допомогою оригамі.[3]
  • Та ж ідея використовується під час доведення того, що дійсні корені рівняння будь-якого степеня ${\displaystyle n}$ можна знайти за допомогою ${\displaystyle (n-2)}$-разових складок оригамі.[4]

• Шан-Гирей А., Флоринский Г. Графическое решение уравнений. Способ Лилля // В.О.Ф.Э.М.. — 1889. — № 61 (24 мая). — С. 6—10.