Правила Худзіти

Нехай задані дві точки ${\displaystyle p_{1}}$ і ${\displaystyle p_{2}}$, тоді аркуш можна скласти так, що ці дві точки будуть лежати на складці.

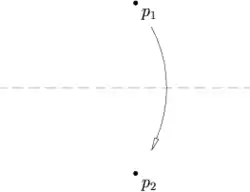
Нехай задані дві точки ${\displaystyle p_{1}}$ і ${\displaystyle p_{2}}$, тоді аркуш можна скласти так, що одна точка перейде в другу.

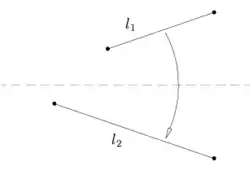
Нехай задані дві прямі ${\displaystyle l_{1}}$ і ${\displaystyle l_{2}}$, тоді аркуш можна скласти таким чином, що одна пряма перейде в другу.

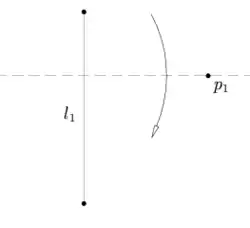
Нехай задані пряма ${\displaystyle l_{1}}$ і точка ${\displaystyle p_{1}}$, тоді аркуш можна скласти так, що точка пройде через складку, а пряма перейде сама в себе (тобто лінія складки буде їй перпендикулярна).

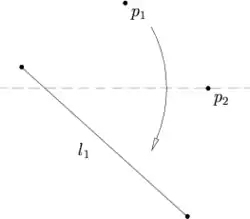
Нехай задані пряма ${\displaystyle l_{1}}$ і дві точки ${\displaystyle p_{1}}$ і ${\displaystyle p_{2}}$, тоді аркуш можна скласти так, що точка ${\displaystyle p_{2}}$ потрапить на складку, а ${\displaystyle p_{1}}$ на пряму ${\displaystyle l_{1}}$.

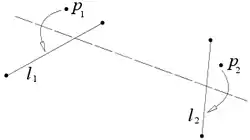
Нехай задані дві прямі ${\displaystyle l_{1}}$ і ${\displaystyle l_{2}}$ і дві точки ${\displaystyle p_{1}}$ і ${\displaystyle p_{2}}$, тоді аркуш можна скласти так, що точка ${\displaystyle p_{1}}$ потрапить на пряму ${\displaystyle l_{1}}$, а точка ${\displaystyle p_{2}}$ на пряму ${\displaystyle l_{2}}$.

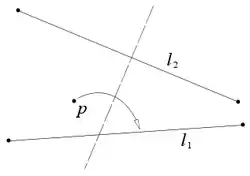
Нехай задані дві прямі ${\displaystyle l_{1}}$ і ${\displaystyle l_{2}}$ і точка ${\displaystyle p}$, тоді аркуш можна скласти так, що точка p потрапить на пряму ${\displaystyle l_{1}}$, а пряма ${\displaystyle l_{2}}$ перейде сама в себе (тобто лінія складки буде їй перпендикулярна).

Всі складки в цьому списку можна отримати як результат послідовного застосування правила номер 6. Тобто для математика вони нічого не додають, однак дозволяють зменшити кількість згинів. Система з семи правил є повною, тобто вона описує всі можливі способи отримання однієї нової складки на аркуші паперу шляхом сполучення вже існуючих різних елементів аркуша. Це останнє ствердження було доведено Робертом Ленгом[1].