Метод рухливих клітинних автоматів

Об'єкт (ліворуч) описується у вигляді набору взаємодіючих автоматів (у центрі). Праворуч представлено поле швидкостей автоматів.

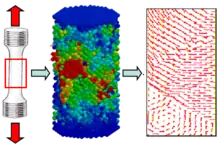
У рамках методу MCA об'єкт моделювання описується як набір взаємодіючих елементів / автоматів. Динаміка безлічі автоматів визначається силами їх взаємодії і правилами для зміни їх стану. Еволюція цієї системи в просторі і в часі визначається рівняннями руху. Сили взаємодії та правила для зв'язаних елементів визначаються функціями відгуку автомата. Ці функції задаються для кожного автомата. Протягом руху автомата наступні нові параметри клітинного автомата розраховуються: Rⁱ - радіус-вектор автомата; Vⁱ - швидкість автомата; ${\displaystyle \omega }$ⁱ - кутова швидкість автомата; ${\displaystyle \theta }$ⁱ - вектор повороту автомата; mⁱ - маса автомата; Jⁱ - момент інерції автомата.

Кожен автомат має декілька сусідів

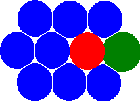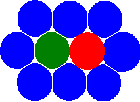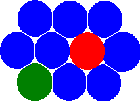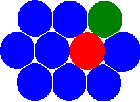
Нова концепція методу MCA заснована на уявленні стану пари автоматів (пов'язує пару взаємодіючих автоматів) у додаток до звичайного стану окремого автомата. Зауважимо що облік цього визначення дозволяє перейти від статичної сіткової концепції до концепції сусідів. В результаті цього, автомати мають можливість змінювати своїх сусідів шляхом перемикання стану (залежностей) пар.

Введення нового типу стану вимагає нового параметра використовується як критерію перемикання в стан пов'язані. Це визначається як параметр перекриття автоматів h^ij. І так, зв'язок клітинних автоматів характеризується величиною їх перекриття.

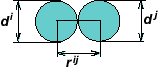
Початкова структура формується установкою властивостей особливого зв'язку між кожною парою сусідніх елементів.

Пара автоматів ij зліва знаходяться у зв'язаному стані, справа - в незв'язаному.

У порівнянні з методом класичних клітинних автоматами в методі MCA не тільки одиничний автомат але і такожзв'язку автоматів можуть переключатися. Відповідно до концепції бістабільних автоматів вводиться два стани пари (взаємозв'язок):

Отже,зміна стану зв'язку пари визначається відносним рухом автоматів, і середовище формується такими парами може бути названабістабільної середовищем.

Еволюція MCA середовища описується наступнимирівняннями трансляційного руху:

${\displaystyle {d^{2}h^{ij} \over dt^{2}}=\left({1 \over m^{i}}+{1 \over m^{j}}\right)p^{ij}+\sum _{k\neq j}C(ij,ik)\psi (\alpha _{ij,ik}){1 \over m^{i}}p^{ik}+\sum _{\ell \neq i}C(ij,j\ell )\psi (\alpha _{ij,j\ell }){1 \over m^{j}}p^{j\ell }}$

Облік сил, що діють між автоматами ij з боку їхніх сусідів.

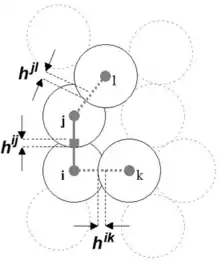
Тут mⁱ це маса автомата i, p^ij це центральна сила діє між автоматами і та j, C (ij,ik) це особливий коефіцієнт асоційований з перенесенням параметра h з пари ij до ik, ψ (α_ij,ik) це кут між напрямками ij і ik.

Обертальні рухи також можуть бути враховані з точністю обмеженою розміром клітинного автомата. Рівняння обертального руху можуть бути записані таким чином:

${\displaystyle {d^{2}\theta ^{ij} \over dt^{2}}=\left({q^{ij} \over J^{i}}+{q^{ji} \over J^{j}}\right)\tau ^{ij}+\sum _{k\neq j}S(ij,ik){q^{ik} \over J^{i}}\tau ^{ik}+\sum _{l\neq j}S(ij,jl){q^{jl} \over J^{j}}\tau ^{jl}}$

Тут Θ^ij кут відносного повороту (це параметр переключення подібно h^ij трансляційного руху), q^ij(ji) це відстань від центру автомата i (j) до точки контакту з автоматом j (i) (кутовий момент), τ^ij це парне тангенціальне взаємодія, S (ij, ik (jl)) це особливий коефіцієнт асоційований з параметром перенесення Θ від однієї пари до іншої (це схоже на C (ij, ik (jl)) з рівнянь трансляційного руху).

Слід зазначити, що рівняння повністю аналогічні рівнянням руху для багато-часткової середовища.

Обертання тіла як цілого не призводить до деформації між автоматами

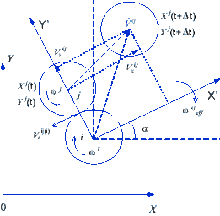
Зсув пари автоматів Безрозмірний параметр деформації для усуненняi j пари автоматів записується як:

${\displaystyle \varepsilon ^{ij}={h^{ij} \over r_{0}^{ij}}={\left(q^{ij}+q^{ji}\right)-\left(d^{i}+d^{j}\right){\big /}2 \over \left(d^{i}+d^{j}\right){\big /}2}}$

У цьому випадку:

${\displaystyle \left(\Delta {\varepsilon ^{i(j)}}+\Delta {\varepsilon ^{j(i)}}\right){\left(d^{i}+d^{j}\right) \over 2}=V_{n}^{ij}\Delta {t}}$

де Δt тимчасової крок, V_n^ij - залежна швидкість. Обертання пари автоматів може бути пораховано аналогічно з зв'язком останнього змішання.

Деформація визначається величиною перекриття автоматів

Існує два типи функцій відгуку автоматів

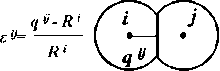
Параметр ε^ij використовується як міра деформації автомата i взаємодіє з автоматом j. Де q^ij - відстань від центру автомата i до точки його контакту з автоматом j; Rⁱ = dⁱ / 2 (dⁱ - розмір автомата i).

Наприклад титановий зразок при циклічному навантаженні (розтяг-стиск). Діаграма деформування показана на наступному малюнку:

схема навантаження	діаграма деформування
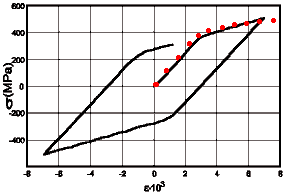	(Червоні точки - експериментальні дані)

Завдяки рухливості кожного автоматаметод MCA дозволяє безпосередньо враховувати такі події як:

• Перемішування мас
• Ефект проникнення
• Хімічні реакції
• Інтенсивні деформації
• Фазові перетворення
• Накопичення ушкоджень
• Фрагментація і тріщини
• Генерація і розвиток ушкоджень

Використовуючи різні граничні умови різних типів (жорсткі, пружні, в'язко-пружні, т.д.) можна імітувати різні властивості навколишнього середовища, що містить модельовану систему. Можна моделювати різні режими механічного навантаження (розтяг, стиск, зсув, т.д.) за допомогою налаштувань додаткових станів на кордонах.

• Psakhie, S.G.; Horie, Y.; Korostelev, S.Yu.; Smolin, A.Yu.; Dmitriev, A.I.; Shilko, E.V.; Alekseev, S.V. (1995). Method of movable cellular automata as a tool for simulation within the framework of mesomechanics. Russian Physics Journal (Springer New York) 38 (11): 1157-1168. doi:10.1007/BF00559396.
• Псахье, С.Г.; Коростелев, С.Ю.; Смолин, А.Ю.; Дмитриев, А.И.; Шилько, Е.В.; Моисеенко, Д.Д.; Татаринцев, Е.М.; Алексеев, С.В. (1998). Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов. Физическая мезомеханика (Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН)) 1 (1): 95-108. Процитовано 3 березня 2010.
• Псахье, С.Г.; Остермайер, Г.П.; Дмитриев, А.И.; Шилько, Е.В.; Смолин, А.Ю.; Коростелев, С.Ю. (2000). Метод подвижных клеточных автоматов как новое направление дискретной вычислительной механики. I. Теоретическое описание. Физическая мезомеханика (Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН)) 3 (2): 5–13. Процитовано 3 березня 2010.
• Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Yu.; Smolin, A.Yu.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S.; Spegel, M.; Zavsek, S. (December 2001). Movable cellular automata method for simulating materials with mesostructure. Theoretical and Applied Fracture Mechanics (Elsevier Science Ltd.) 37 (1-3): 311-334. doi:10.1016/S0167-8442(01)00079-9. Архів оригіналу за 19 липня 2011.
• Псахье, С.Г.; Смолин, А.Ю.; Стефанов, Ю.П.; Макаров, П.В.; Чертов, М.А. (2004). Моделирование поведения сложных сред на основе совместного использования дискретного и континуального подходов. Письма в ЖТФ 30 (17): 7–13. Процитовано 3 березня 2010.
• Shimizu, Y.; Hart, R.; Cundall, P. (2004). Numerical modeling in Micromechanics via Particle Methods. ISBN 9058096793. Процитовано 3 березня 2010.
• Gnecco, E.; Meyer E. (Eds.) (2007). Fundamentals of friction and wear on the Nanoscale. ISBN 9783540368069. Процитовано 3 березня 2010.
• Yunliang, Tan; Guirong, Teng; Haitao, Li. MCA Model for Simulating the Failure of Microinhomogeneous Materials. Journal of Nanomaterials (Hindawi Publishing Corporation) 2008: 1-7. doi:10.1155/2008/946038. 946038.
• Фомин, В.М.; Андреев А.Н. и др. (2008). Механика - от дискретного к сплошному. Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича. с. 344. ISBN 978-5-7692-0974-1. Архів оригіналу за 06.10.2011. Процитовано 3.03.2010.
• Смолин, А.Ю.; Роман, Н.В.; Добрынин, С.А.; Псахье, С.Г. (2009). О вращательном движении в методе подвижных клеточных автоматов. Физическая мезомеханика (Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН)) 12 (2): 17–22. Процитовано 3 березня 2010.
• Popov, Valentin L. (2009). Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation). Springer Berlin Heidelberg. ISBN 9783540888369. doi:10.1007/978-3-540-88837-6. . doi:10.1007/978-3-540-88837-6. Пропущений або порожній |title= (довідка)
• Добрынин, С.А. (2010). Развитие метода подвижных клеточных автоматов для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел. Томск: Диссертация … кандидата физико-математических наук. с. 130. Процитовано 3.03.2010.
• Добрынин, Сергей (2011). Компьютерное моделирование методом подвижных клеточных автоматов. Saarbrücken Germany: LAP LAMBERT Academic Publishing. с. 132. ISBN 978-3-8443-5954-1. Процитовано 19.11.2011.

• MCA software package
• Програма для моделювання матеріалів в дискретно континуальному підході «FEM+MCA»: Номер державної реєстрації в ОФАП (Патент): 50208802297 / Смолин А. Ю., Зелепугин С. А., Добрынин С. А.; заявник та організація-розробник рос. ГОУ ВПО Томский государственный университет. — зарег. 28.11.2008; свідоцтво ОФАП № 11826 від 01.12.2008.

• Механіка суцільних середовищ
• Механіка руйнування
• Теорія пружності
• Перідінаміка
• Імітаційне моделювання
• Метод дискретного елемента
• Клітинний автомат
• Метод скінченних елементів
• Метод скінченних різниць