Мішаний добуток

• Змішаний добуток кососиметричний по відношенню до всіх своїх аргументів:

${\displaystyle (\ \mathbf {a} ,\ \mathbf {b} ,\ \mathbf {c} )=(\ \mathbf {b} ,\ \mathbf {c} ,\ \mathbf {a} )=(\ \mathbf {c} ,\ \mathbf {a} ,\ \mathbf {b} )=-(\ \mathbf {b} ,\ \mathbf {a} ,\ \mathbf {c} )=-(\ \mathbf {c} ,\ \mathbf {b} ,\ \mathbf {a} )=-(\ \mathbf {a} ,\ \mathbf {c} ,\ \mathbf {b} );}$

т. тобто перестановка будь-яких двох співмножників міняє знак добутку. Звідси випливає, що

${\displaystyle \ \langle \ \mathbf {a} ,[\ \mathbf {b} ,\ \mathbf {c} ]\ \rangle =\ \langle [\ \mathbf {a} ,\ \mathbf {b} ],\ \mathbf {c} \ \rangle }$

• Змішаний добуток ${\displaystyle (\ \mathbf {a} ,\ \mathbf {b} ,\ \mathbf {c} )}$ в правій декартовій системі координат (в ортонормованому базисі) дорівнює визначнику матриці, складеної з векторів ${\displaystyle \ \mathbf {a} ,\ \mathbf {b} }$ та ${\displaystyle \ \mathbf {c} }$:

${\displaystyle (\mathbf {a} ,\mathbf {b} ,\mathbf {c} )={\begin{vmatrix}a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\\c_{x}&c_{y}&c_{z}\end{vmatrix}}.}$

• Змішаний добуток${\displaystyle (\ \mathbf {a} ,\ \mathbf {b} ,\ \mathbf {c} )}$ в лівій декартовій системі координат (в ортонормованому базисі) дорівнює визначнику матриці, складеної з векторів ${\displaystyle \ \mathbf {a} ,\ \mathbf {b} }$ та ${\displaystyle \ \mathbf {c} }$, взятому зі знаком «мінус»:

${\displaystyle (\mathbf {a} ,\mathbf {b} ,\mathbf {c} )=-{\begin{vmatrix}a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\\c_{x}&c_{y}&c_{z}\end{vmatrix}}.}$

зокрема,

• Якщо якісь два вектори колінеарні, то з будь-яким третім вектором вони утворюють мішаний добуток, що дорівнює нулю.
• Якщо три вектори лінійно залежні (т. тобто компланарні, лежать в одній площині), то їх мішаний добуток дорівнює нулю.
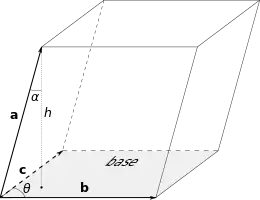
• Геометричний сенс — мішаний добуток ${\displaystyle (\ \mathbf {a} ,\ \mathbf {b} ,\ \mathbf {c} )}$ за абсолютним значенням дорівнює об'єму паралелепіпеда (див. малюнок), утвореного векторами ${\displaystyle \ \mathbf {a} ,\ \mathbf {b} }$ та ${\displaystyle \ \mathbf {c} }$; знак залежить від того, чи є ця трійка векторів права або ліва.
• Квадрат змішаного добутку векторів дорівнює визначнику Грама, що визначається ними[1]^:215.

Три вектора, що визначають паралелепіпед.

• Змішаний добуток зручно записується за допомогою символу (тензора) Леві-Чивіти:

${\displaystyle (\mathbf {a} ,\ \mathbf {b} ,\ \mathbf {c} )=\ \sum _{i,j,k}\ \varepsilon _{ijk}a^{i}b^{j}c^{k}}$

(в останній формулі в ортонормированном базисі всі індекси можна писати нижніми; в цьому випадку ця формула абсолютно прямо повторює формулу з визначником, правда, при цьому автоматично виходить множник (-1) для лівих базисів).

Мішаний добуток не є принципово новим математичним поняттям, оскільки процедура його обчислення зводиться до послідовного знаходження скалярного та векторного добутків. Попри це, вивчення мішаного добутку як окремого математичного об'єкта є дуже доцільним, оскільки він часто зустрічається при розгляді різноманітних задач і має низку властивостей, що спрощують їх розв'язання.

Потрійний векторний добуток — векторним добутком одного вектора із векторним добутком двох інших. Має місце така формула:

${\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )\equiv \mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}$.