Намисто Антуана
Намисто Антуана (антуанівська множина[1]) — приклад підмножини евклідового простору, яка гомеоморфна канторовій множині, але при цьому має неоднозв'язне доповнення.

Перша ітерація
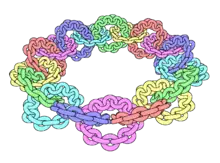
Друга ітерація
Побудова
Намисто будується як перетин спадної послідовності компактних множин:
такої, що кожне є об'єднанням скінченного числа неперетинних повноторів.
Якщо найбільший діаметр повнотора в прямує до нуля при , то перетин:
є компактною цілком незв'язною множиною без ізольованих точок, а отже гомеоморфним канторовій множині.
З іншого боку, можна вибрати послідовність так, що доповнення до отриманого неоднозв'язне, для цього перетин з кожним повнотором у має утворювати замкнутий ланцюг, як на малюнку.
Див. також
Примітки
- Болтянский В.Г., Ефремович В.А.. Наглядная топология. — М. : Наука, 1982. — 160 с. — (Бібліотечка «Квант»)
- Antoine, Louis (1921), «Sur l'homeomorphisme de deux figures et leurs voisinages», Journal Math Pures et appl. 4: 221—325
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.