Повний тор

Повний тор[1] (повнотор[2], повноторій[3]) — тривимірна фігура, обмежена тором, а також топологічний простір, гомеоморфний цій фігурі, тобто прямий добуток $D^{2}\times S^{1}$ двовимірного диска і кола. Неформально, повний тор — бублик, тоді як тор — тільки його поверхня (пустотіла камера колеса).

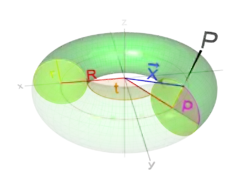
Повний тор

Властивості

Повний тор можна отримати як фігуру обертання круга радіуса $r$ навколо осі, що лежить у площині цього круга і розташована на відстані $R$ від його центра.
Об'єм повного тора як наслідок з другої теореми Гульдіна: $V=2\pi ^{2}Rr^{2}$ , де $r$ — радіус твірного круга, а $R$ — відстань від центра твірного круга до осі обертання (див. рисунок).
Повний тор є тривимірним компактним многовидом із краєм. Цей многовид є зв'язним і орієнтованим.
Повний тор гомотопічно еквівалентний колу $S^{1}$ . Звідси випливає, що повний тор і коло мають однакові фундаментальні групи і групи гомологій:

\pi _{1}(S^{1}\times D^{2})\cong \pi _{1}(S^{1})\cong \mathbb {Z}

H_{k}(S^{1}\times D^{2})\cong H_{k}(S^{1})\cong {\begin{cases}\mathbb {Z} &k=0,1\\0&k\geq 2\end{cases}}

Примітки

Круглов, Володимир. Параболічні та сідлові шарування та розподілення на тривимірних многовидах. Автореферат дисертації (укр.). Процитовано 23 вересня 2020.
Плахта Л.П. IНВАРIАНТИ ВУЗЛIВ, ПОВЕРХНI ВR3I ШАРУВАННЯ // Український математичний журнал. — Київ, 2007. — Т. 59, № 9. — С. 1247. — ISSN 1027-3190. Процитовано 18 грудня 2020.
Пришляк, О. О. (2013). Топологія многовидів. Навчальний посібник (укр.). Київ: Київський національний університет імені Тараса Шевченка.

Література

Фоменко А. Т. Наглядная геометрия и топология — М., 1992.
Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии.— М.: Наука, 1989.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Круглов, Володимир. Параболічні та сідлові шарування та розподілення на тривимірних многовидах. Автореферат дисертації (укр.). Процитовано 23 вересня 2020.

[2] Плахта Л.П. IНВАРIАНТИ ВУЗЛIВ, ПОВЕРХНI ВR3I ШАРУВАННЯ // Український математичний журнал. — Київ, 2007. — Т. 59, № 9. — С. 1247. — ISSN 1027-3190. Процитовано 18 грудня 2020.

[3] Пришляк, О. О. (2013). Топологія многовидів. Навчальний посібник (укр.). Київ: Київський національний університет імені Тараса Шевченка.