Дикий вузол

Вузол називається ручним, якщо він може бути «потовщений», тобто якщо існує його розширення до повного тора S ¹ × D ², який допускає вкладення в 3-сферу. В теорії вузлів і в теорії 3-многовидів часто слово «ручний» опускають.

Вузли, які не є ручними, називаються дикими і можуть мати патологічний поведінку.

Дуга Фокса — Артіна

Дикими є вузли, що містять так звані дуги Фокса — Артіна — деякі прості дуги, отримані диким вкладенням в ${\displaystyle E^{3}}$. Наприклад, для дуги ${\displaystyle L_{1}}$ фундаментальна група ${\displaystyle p_{1}}$(${\displaystyle E^{3}L}$) нетривіальна, для дуги ${\displaystyle L_{2}}$ група ${\displaystyle {\pi }_{1}(E^{3}/L)}$ тривіальна, але саме ${\displaystyle E^{3}/L}$ не гомеоморфне доповненню в ${\displaystyle E^{3}}$ до точки[1].

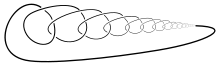
На малюнку наведено дикий вузол з однією дикою (патологічною) точкою. Легко побудувати дикий вузол, що містить кілька патологічних точок, нескінченне число таких точок, і навіть незліченну множину патологічних точок. У книзі Сосинського[2] наведено побудову дикого вузла, патологічні точки якого утворюють множину Кантора.

Можна представити і дикий вузол, що містить більш складну множину — намисто Антуана[2].

• Вузол є ручним тоді і тільки тоді, коли його можна подати у вигляді скінченної ламаної.
• Гладкі вузли є ручними.

• Нетривіальні дикі вузли з'являються й у сферах старших розмірностей. Наприклад, за теоремою про подвійну надбудову, подвійна надбудова над сферою Пуанкаре гомеоморфна стандартній сфері ${\displaystyle \mathbb {S} ^{5}}$. При цьому екватор подвійної надбудови утворює в ${\displaystyle \mathbb {S} ^{5}}$ дикий вузол і його доповнення має нетривіальну фундаментальну групу.

• Дика сфера

• L. H. Kauffman. An invariant of regular isotopy // Transactions of the American Mathematical Society. — American Mathematical Society, 1990. — Т. 318, № 2 (16 грудня).
• А. Б. Сосинский. Узлы. Хронология одной математической теории. — Москва : МЦНМО, 2005. — ISBN 5-94057-220-0.