Напрямні косинуси

Вектор v в просторі ℝ³.

Напрямні косинуси і кути напрямків одиничного вектора v/|v|.

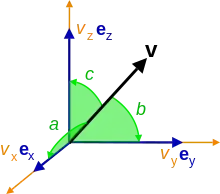
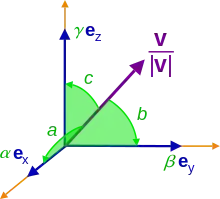
Якщо v є Евклідовим вектором в тривимірному Евклідовому просторі, ℝ³,

${\displaystyle {\mathbf {v} }=v_{\text{x}}\mathbf {e} _{\text{x}}+v_{\text{y}}\mathbf {e} _{\text{y}}+v_{\text{z}}\mathbf {e} _{\text{z}}}$

де e_x, e_y, e_z стандартний базис у декартовій системі координат, тоді напрямні косинуси це:

${\displaystyle {\begin{aligned}\alpha &=\cos a={\frac {{\mathbf {v} }\cdot \mathbf {e} _{\text{x}}}{\left|{\mathbf {v} }\right|}}&={\frac {v_{\text{x}}}{\sqrt {v_{\text{x}}^{2}+v_{\text{y}}^{2}+v_{\text{z}}^{2}}}},\\\beta &=\cos b={\frac {{\mathbf {v} }\cdot \mathbf {e} _{\text{y}}}{\left|{\mathbf {v} }\right|}}&={\frac {v_{\text{y}}}{\sqrt {v_{\text{x}}^{2}+v_{\text{y}}^{2}+v_{\text{z}}^{2}}}},\\\gamma &=\cos c={\frac {{\mathbf {v} }\cdot \mathbf {e} _{\text{z}}}{\left|{\mathbf {v} }\right|}}&={\frac {v_{\text{z}}}{\sqrt {v_{\text{x}}^{2}+v_{\text{y}}^{2}+v_{\text{z}}^{2}}}}.\end{aligned}}}$

Якщо звести в квадрат кожне рівняння і додати отримаємо:

${\displaystyle \cos ^{2}a+\cos ^{2}b+\cos ^{2}c=1\,.}$

Тут, α, β і γ напрямні косинуси Декартової системи координат одиничного вектора v/|v|, а a, b і c є кутами направлення вектора v.

Напрямні кути a, b і c можуть бути гострими або тупими кутами, тобто, 0 ≤ a ≤ π, 0 ≤ b ≤ π і 0 ≤ c ≤ π і вони задають кути утворені між v одиничними базисними векторами, e_x, e_y і e_z.

В більш загальному сенсі, напрямний косинус відноситься до косинуса кута між двома векторами. Вони застосовуються для побудови косинусних матриць повороту, які задають набір ортогональних базисних векторів для задання відомого вектора в іншому базисі.

• D. C. Kay (1988). Tensor Calculus. Schaum’s Outlines. McGraw Hill. с. 18–19. ISBN 0-07-033484-6.
• M. R. Spiegel; S. Lipschutz; D. Spellman (2009). Vector analysis. Schaum’s Outlines (вид. 2nd). McGraw Hill. с. 15, 25. ISBN 978-0-07-161545-7.
• J.R. Tyldesley (1975). An introduction to tensor analysis for engineers and applied scientists. Longman. с. 5. ISBN 0-582-44355-5.

• Tang, K.T. (2006). Mathematical Methods for Engineers and Scientists 2. Springer. с. 13. ISBN 3-540-30268-9.
• Weisstein, Eric W. Direction Cosine(англ.) на сайті Wolfram MathWorld.