Нестійкість Релея — Тейлора
Нестійкість Релея - Тейлора - виникає між двома контактуючими суцільними середовищами різної щільності, коли більш важка рідина штовхає більш легку. Прикладом такої нестійкості може служити нестійкість краплі води на поверхні олії - вода буде намагатися проникнути крізь олію.
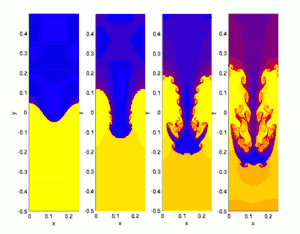
Основним параметром, що визначає швидкість розвитку цієї нестабільності є число Атвуда.
Аналітичний опис
Задача про нестійкості Релея — Тейлора має аналітичне рішення в рамках лінійної теорії стійкості.
Нехай два протяжних плоских горизонтальних шару рідини розташовані в полі тяжіння один над одним, причому більш важка рідина 1 знаходиться вгорі (на ілюстрації — синій колір), щільності рідин . Верхня і нижня межі — тверді. Для простоти зручно користуватися моделлю нев'язкої нестисливої рідини, тоді система описується рівнянням Ейлера:
Надалі компоненти швидкості визначаються як . Цілком очевидно, що рівноважне рішення () задовольняє моделі, при цьому з рівняння Ейлера для тиску виходить наступне:
Звідки визначається рівноважний розподіл тиску (відомий результат для тиску стовпа рідини):
Внесемо в рівноважний стан малі збурення. Нехай швидкість настільки мала, що можна знехтувати нелінійним доданком в рівнянні Ейлера, а тиск має вигляд , де . Тоді отримаємо лінійну систему рівнянь для малих збурень (далі штрих у тиску опущений):
Граничні умови задаються виходячи з міркувань рівності z-компонент швидкості рідин 1 і 2 на межі розділу і наявності поверхневого натягу. На верхній і нижній межах, тому що рідина ідеальна, працюють умови непротікання. Зручно прийняти координату кордону розділу в рівновазі за 0. На ній виконується кінематична умова
і динамічна умова
Умова непротікання верхньої і нижньої меж:
де — величина відхилення кордону від незбуреної, — коефіцієнт поверхневого натягу. Отримана завдання для збурень легко вирішується. Припустимо, що збурення мають вигляд:
де — швидкість росту (інкремент) обурення, — компоненти хвильового вектора обурення кордону.
З рівняння Ейлера виражається :
а умова дає рівняння Лапласа для тиску. У результаті, швидкість течії із завдання вдається виключити. Залишається лінійне рівняння:
з граничними умовами:
Рішення рівняння Лапласа для тиску:
Константи визначаються з кінематичного умови. Динамічне умова дає зв'язок між інкремент і модулем хвильового вектора
звідки безпосередньо випливає вираз для критичного хвильового числа збурень (при ):
- .
Якщо довжина хвилі більша за критичну, то обурення кордону будуть наростати.
У граничному випадку нескінченно глибоких шарів () найбільша швидкість росту збурень досягається при хвильовому числі
- .
У тонких шарах ():
- .
Література
- Лабунцов Д.А., Ягов В.В. Механіка двофазних систем. / / М.: Видавництво МЕІ, 2000. - С. 143-146.
- Векштейн Г.Є. Фізика суцільних середовищ в завдання. / / М.: Інститут комп'ютерних досліджень, 2002. - С. 109-111.