Ідеальна рідина

Ідеа́льна рідина́ — уявна рідина (або газ), позбавлена в'язкості і теплопровідності та процесів, пов'язаних з ними. У ідеальної рідини відсутнє внутрішнє тертя, тобто немає дотичних напружень між двома сусідніми шарами, вона неперервна і не має структури. Така ідеалізація допустима у багатьох випадках для течій, що розглядаються в гідроаеромеханіці, і дає хороший опис реальних течій рідин і газів на достатній відстані від омиваних твердих поверхонь і поверхонь розділу з нерухомим середовищем. В механіці рідини та газу при математичному моделюванні течій використовують два типи ідеальних рідин — ідеальна нестислива рідина та ідеальна стислива рідина. В аеродинаміці модель нестисливої рідини успішно використовують при аналізі рухів зі швидкостями, меншими від швидкості звуку у відповідній реальній рідині. Вивчення рухів тіл в стисливій рідині при високих швидкостях є предметом газової динаміки. Детальний аналіз можливостей двох вказаних моделей приведено в літературі[1].

Механіка суцільних середовищ
Закони класичної механіки Закон збереження маси • Закон збереження імпульсу • Закон збереження енергії • Нерівність Клаузіуса
Механіка ДТТ Тверде тіло: Напруження • Деформація • Теорія малих деформацій • Теорія великих деформацій • Теорія пружності • Механіка контактної взаємодії • Опір матеріалів • Теорія пластичності • Механіка руйнування
Механіка рідин та газів Флюїд: Тиск • Гідростатика (закон Архімеда; закон Паскаля) • Гідродинаміка (закон Бернуллі) • В'язкість (ньютонівська рідина; неньютонівська рідина) Рідина: Поверхневий натяг • Капілярний ефект Газ: Рівняння стану ідеального газу (Закон Гей-Люссака; Закон Бойля — Маріотта; закон Шарля) • Реальний газ Плазма
Реологія В'язкоеластичність • Розумні рідини (Магнетореологічна рідина, Електрореологічна рідина, Феромагнітна рідина) • Реометрія
Основні рівняння Рівняння неперервності • Рівняння Ейлера • Рівняння Нав'є — Стокса • Рівняння дифузії • Закон Гука
Вчені Ньютон • Стокс • Нав'є • Коші • Гук, Бернуллі

Поняття ідеальної стисливої рідини досить широко використовується при моделюванні процесів генерування та поширення звуку, хоча в таких процесах швидкості руху частинок рідини або газу значно менші від швидкості звуку[2].

Рух ідеальної рідини описується рівняннями Ейлера і відбувається адіабатично, тобто ентропія будь-якого елементу рідини залишається незмінною.

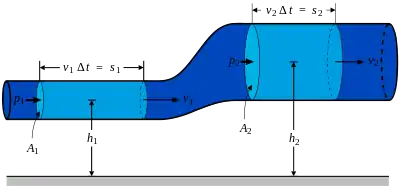
Вздовж струменів рідини виконується Закон Бернуллі

${\displaystyle {\frac {v^{2}}{2}}+\psi +w={\text{const}}}$,

де ${\displaystyle \psi }$ — потенціал зовнішніх сил, а w — ентальпія одиниці маси рідини. Стала, яка входить в закон Коші-Бернуллі, є сталою лише для даного струменя і може мати різні значення в різних точках рідини. Для стаціонарного руху ця величина єдина для всієї області існування потоку. При вивченні рухів суцільних середовищ (рідин, газів, твердих деформовних тіл) для представлення поля швидкостей використовують теорему Гельмгольця, згідно якої будь-яке векторне поле (наприклад, поле швидкостей частинок середовища ${\displaystyle \mathbf {v} }$) може бути представлене в вигляді

${\displaystyle \mathbf {v} =\nabla \varphi +rot\mathbf {A} }$

Тут функції ${\displaystyle \varphi }$ та ${\displaystyle \mathbf {A} }$ називаються відповідно скалярним та векторним потенціалом поля швидкостей.

Якщо в певній течії векторний потенціал дорівнює нулю, таку течію називають потенціальною. Течію, в якій дорівнює нулю скалярний потенціал, називають соленоїдальною.

Для потенціальної ідеальної рідини справедливий закон Бернуллі, який є частковим випадком закону Коші-Бернуллі. На відміну від закону Коші-Бернуллі закон Бернуллі справедливий у всьому об'ємі рідини, а не лише вздовж струменя.