Квадратна ґратка
Квадратна ґратка — це вид ґратки в двовимірному евклідовому просторі. Ґратка є двовимірною версією цілочисельної ґратки і позначається Z2[1]. Ґратка є однією з п'яти типів двовимірних ґраток, класифікованих за групами симетрії[2]. Група симетрії ґратки в позначеннях IUC — p4m [3], в нотації Коксетера — [4,4][4], а в орбіфолдній нотації — *442[5].
 | |
| Вертикальна | Діагональна |
|---|---|
Дві орієнтації ґратки найпопулярніші. Зазвичай квадрати решітки розміщуються так, що сторони квадрата вертикальні і горизонтальні (будемо називати це вертикальною ґраткою), або сторони квадратів розташовані під кутом 45° до осей. В останньому випадку ґратку іноді називають центрованою квадратною ґраткою[6].
Симетрія
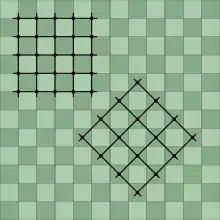
Симетрія квадратної решітки — це група орнаменту p4m. Орнамент з цієї ґраткою симетрії перенесення не може мати вищого степеня симетрії, ніж сама ґратка, але може мати менший степінь. Вертикальну квадратну ґратку можна розглядати як діагональну ґратку з розміром сітки в √2 рази більшим, центри якої містяться в центрах квадратів. Відповідно, після додавання центрів квадратів у квадрати вертикальної ґратки отримуємо ґратку в √2 рази меншу від початкової ґратки. Орнамент з 4-кратною обертовою симетрією має квадратну ґратку 4-кратних центрів обертання, яка √2 рази дрібніша і розташована діагонально відносно початкової ґратки симетрії перенесення.
Стосовно осей відображення існує три можливих ситуації:
- Відсутність симетрії. Це група шпалер p4.
- В чотирьох напрямках. Це група шпалер p4m.
- У двох перпендикулярних напрямках. Це група шпалер p4g. Точки перетину осей відображення утворюють квадратну ґратку, яка за розмірами та за напрямами збігається з квадратною ґраткою центрів обертання.
| p4, [4,4]+, (442) | p4g, [4,4+], (4*2) | p4m, [4,4], (*442) |
|---|---|---|
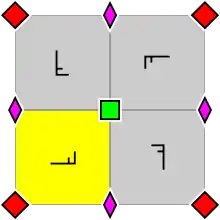 |
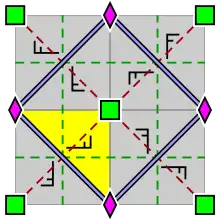 |
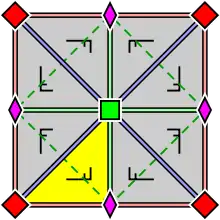 |
| Група шпалер p4, з розташуванням усередині примітивної комірки 2 — і 4-кратних центрів обертання (істинне і для p4g і p4m). Фундаментальну область показано жовтим кольором. | Група шпалер p4g. Є осі відображення в двох напрямках, які не проходять через 4-кратні центри обертання. | Група шпалер p4m. Є осі відображення в чотирьох напрямках, що проходять через 4-кратні центри обертання. У двох напрямках осі відображення орієнтовані так само і з тією ж щільністю, що й для p4g, але зсунуті. У двох напрямах вони в √2 рази щільніші. |
Див. також
- Центроване квадратне число
- Евклідів сад
- Гаусові числа
- Шестикутна ґратка
- Квінкункс
- Квадратний паркет
Примітки
- Conway, Sloane, 1999, с. 106.
- Golubitsky, Stewart, 2003, с. 129.
- Field, Golubitsky, 2009, с. 47.
- Johnson, Weiss, 1999, с. 1307–1336, см. стр 1320.
- Schattschneider, Senechal, 2004, с. 53–72.
- Johnston, Richman, 1997, с. 159.
Література
- Conway John, Sloane Neil J. A. Sphere Packings, Lattices and Groups. — 1999. — С. 106. — ISBN 9780387985855.
- Golubitsky Martin, Stewart Ian. The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space. — 2003. — Т. 200. — С. 129. — (Progress in Mathematics) — ISBN 9783764321710.
- Michael Field, Golubitsky Martin. Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature. — 2nd. — 2009. — С. 47. — ISBN 9780898717709.
- Johnson Norman W., Weiss Asia Ivić. Quadratic integers and Coxeter groups // Canadian Journal of Mathematics. — 1999. — Т. 51 (22 листопада). — С. 1307–1336. — DOI:.. См. начало страницы 1320.
- Schattschneider Doris, Senechal Marjorie. Tilings // Handbook of Discrete and Computational Geometry. — 2nd. — 2004. — С. 53–72. — (Discrete Mathematics and Its Applications) — ISBN 9781420035315.. Див. таблицю на стор. 62.
- Johnston Bernard L., Richman Fred. Numbers and Symmetry: An Introduction to Algebra. — 1997. — С. 159. — ISBN 9780849303012.