Окіл (теорія графів)
В теорії графів суміжною вершиною вершини v називається вершина, поєднана з v ребром. Околом вершини v в графі G називається породжений підграф графа G, що складається з усіх вершин, сполучених з v і всіх ребер, що з'єднують дві таких вершини. Наприклад, малюнок показує граф з 6 вершинами і 7 ребрами. Вершина 5 суміжна вершинам 1, 2, і 4, але не суміжна вершинам 3 і 6. Окіл вершини 5 — це граф з трьома вершинами 1, 2, і 4, і одним ребром, що з'єднує вершини 1 і 2.
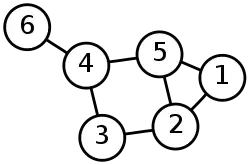
Окіл часто позначається як NG(v) або (якщо відомо, про який граф йде мова) N(v). Те ж саме позначення околу може використовуватися для посилання на множину суміжних вершин, а не на відповідний породжений підграф. Окіл, описаний вище не включає саму вершину v і про цей окіл говорять як про відкритий окіл вершини v. Можна визначити окіл, що включає v. У цьому випадку окіл називається замкненим та позначається як NG[v]. Якщо не вказано явно, то окіл є відкритим.
Околи можна використовувати для представлення графів в комп'ютерних алгоритмах через список суміжності та матрицю суміжності. Околи використовуються також в коефіцієнті кластеризації графа, який вимірює середню густину його околів. До того ж, багато важливих класів графів можна визначити властивостями його околи або взаємною симетрією околів.
Ізольована вершина не має суміжних вершин. Степінь вершини дорівнює числу суміжних вершин. Спеціальним випадком є петля, що з'єднує вершину з тією ж самою вершиною. Якщо таке ребро існує, вершина належить власному околу.
Локальні властивості графа
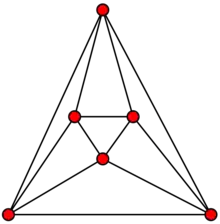
Якщо всі вершини графа G мають околи, ізоморфні деякому графа H, кажуть, що G є локальним графом H, і якщо всі вершини G мають околи, що належать деякому сімейству графів F, кажуть, що G є локальним графом F (Hell 1978, Sedlacek 1983). Наприклад, у графі октаедра, показаному на малюнку, кожна вершина має окіл, ізоморфний циклу з чотирьох вершин, так що октаедр є локально C4.
Наприклад:
- Будь-який повний граф Kn є локально графом Kn-1. Єдині графи, які локально повні — це недоладне об'єднання повних графів.
- Граф Турана T (rs,r) локально еквівалентнийT ((r-1) s, r-1). Тобто, будь-який граф Турана локально є графом Турана.
- Будь-який планарний граф локально зовніпланарний. Однак, не всякий локально зовніпланарний граф є планарним.
- Граф є графом без трикутників в тому, і лише в тому випадку, якщо він локально незалежний.
- Будь-який k-хроматичний граф локально (k-1) -хроматичний. Будь-який локально k-хроматичний граф має хроматичне число (Wigderson, 1983)
- Якщо сімейство графів F замкнуто щодо операції взяття породжених підграфів, то будь-який граф в F локально теж F. наприклад, будь-який хордальний граф локально хордальний, будь-який досконалий граф локально досконалий, будь-який граф порівняння є локально графом порівняння.
- Граф локально циклічний якщо будь-який окіл є циклом. Наприклад, граф октаедра є єдиним локально C4 графом, граф ікосаедра є єдиним локально C5 графом, а граф Пейли 13-го порядку локально є C6. Локально циклічні графи, відмінні від K4, — це в точності графи, що лежать в основі тріангуляції Вітні, що здійснює вкладення графів в поверхню таким чином, що грані при впровадженні відповідають клікам графа (Hartsfeld & Ringel, 1981; Larrión, Neumann-Lara & Pizaña, 2002; Malnič & Mohar, 1992). Локально циклічні графи можуть до ребер (Seress та Szabó, 1995).
- Графи без клешень — це графи, локально вільні від трикутників. Тобто, для всіх вершин, доповнення графа околів вершини не містить трикутників. Граф, який є локальним графом H без клешень тоді і лише тоді, коли число незалежності графа H не більш двох. Наприклад, граф правильного ікосаедра не містить клешень, оскільки він локально C5 та число незалежності C5 дорівнює двом.
Множина сусідів
Для множини A вершин, окіл A — це об'єднання околів вершин, так що вона містить всі вершини, зв'язані з принаймні одним елементом A.
Кажуть, що множина A вершин графа є модулем, якщо всі вершини A мають ту ж саму множину околів поза A. Будь який граф має унікальне рекурсивне розкладання на модулі, зване модульним розкладанням, яке можна побудувати з графа за лінійний час. Алгоритм модульного розкладання застосовується в інших алгоритмах для графів, включаючи розпізнавання графа порівняння.
Посилання
- Hartsfeld, Nora; Ringel, Gerhard (1991). Clean triangulations. Combinatorica 11 (2): 145–155. doi:10.1007/BF01206358..
- Hell, Pavol (1978). Graphs with given neighborhoods I. Problems Combinatories et theorie des graphes. Colloque internationaux C.N.R.S. 260. с. 219–223..
- Larrión, F.; Neumann-Lara, V.; Pizaña, M. A. (2002). Whitney triangulations, local girth and iterated clique graphs. Discrete Mathematics 258: 123–135. doi:10.1016/S0012-365X(02)00266-2..
- Malnič, Aleksander; Mohar, Bojan (1992). Generating locally cyclic triangulations of surfaces. Journal of Combinatorial Theory, Series B 56 (2): 147–164. doi:10.1016/0095-8956(92)90015-P..
- Sedlacek, J. (1983). On local properties of finite graphs. Graph Theory, Lagów. Lecture Notes in Mathematics 1018. Springer-Verlag. с. 242–247. ISBN 978-3-540-12687-4. doi:10.1007/BFb0071634..
- Seress, Ákos; Szabó, Tibor (1995). Dense graphs with cycle neighborhoods. Journal of Combinatorial Theory, Series B 63 (2): 281–293. doi:10.1006/jctb.1995.1020. Архів оригіналу за 30 серпня 2005. Процитовано 5 червня 2015..
- Wigderson, Avi (1983). Improving the performance guarantee for approximate graph coloring. Journal of the ACM 30 (4): 729–735. doi:10.1145/2157.2158..