Оптимізація на основі моделювання
Оптимізація на основі моделювання (також відома як оптимізація моделювання) інтегрує методи оптимізації в цифрове моделювання та аналіз. Через складність моделювання оцінка цільової функції (функції втрат) може стати дорогою та важкою. Зазвичай базова імітаційна модель є стохастичною, тому цільову функцію необхідно оцінити за допомогою методів статистичної оцінки (в методології моделювання називають вихідним аналізом).
Після того, як система змодельована математично, комп'ютерне моделювання надає інформацію про її поведінку. Для підвищення продуктивності системи використовують методи параметричного моделювання. У цьому методі введення кожної змінної варіюється, а інші параметри залишаються постійними, і спостерігається вплив на ціль проєктування. Це трудомісткий метод, який частково покращує продуктивність. Щоб отримати оптимальне рішення з мінімальними витратами часу та обчислень, завдання вирішується ітеративно, при цьому на кожній ітерації рішення наближається до оптимального. Такі методи відомі як «чисельна оптимізація» або «оптимізація на основі моделювання».[1]
Ціль імітаційного експерименту полягає в тому, щоб оцінити вплив різних значень вхідних змінних на систему. Хоча іноді, інтерес полягає в тому, щоб знайти оптимальне значення для вхідних змінних з погляду результатів системи. Одним із способів пошуку оптимального значення, може бути проведення експериментів з моделювання для всіх можливих вхідних змінних. Цей підхід не завжди є практичним через кілька можливих ситуацій, також цей підхід ускладнює проведення експериментів для кожного сценарію. Наприклад, імітаційна модель може бути занадто складною та дорогою для запуску при неоптимальних значеннях вхідних змінних або може бути занадто багато можливих значень для вхідних змінних. У цих випадках ціль полягає в тому, щоб знайти оптимальні значення для вхідних змінних, а не пробувати всі можливі значення. Цей процес називається оптимізацією моделювання.[2]
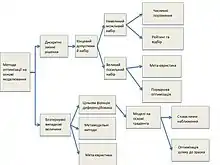
Конкретні методи оптимізації, засновані на моделюванні, можуть бути обрані відповідно до рис. 1 на основі типів змінних рішень.[3]
Оптимізація існує у двох основних галузях дослідження операцій:
Параметрична оптимізація (статична) — полягає в тому, щоб знайти значення параметрів, які є статичними для всіх станів та максимізують або мінімізують функцію. У цьому випадку можна використовувати математичне програмування, наприклад, лінійне програмування. У цьому сценарії симуляція допомагає, коли параметри містять шум або оцінка проблеми вимагатиме надмірного комп'ютерного часу через її складність.[4]
Управління оптимізацією (динамічне) — в основному використовується в інформатиці та електротехніці. Оптимальне керування визначається для кожного стану і результати змінюються в кожному з них. Можна використовувати математичне програмування і динамічне. У цьому сценарії моделювання може генерувати випадкові вибірки, вирішувати складні та великомасштабні проблеми.[4]
Методи оптимізації на основі моделювання
Деякі важливі підходи до оптимізації моделювання наводяться нижче.[5][6]
Статистичний рейтинг і методи відбору (R/S)
Методи ранжування та відбору призначені для завдань, у яких альтернативи фіксовані та відомі, а моделювання використовується для оцінки продуктивності системи. У налаштуванні оптимізації моделювання, застосовні методи включають підходи зони байдужості, оптимальні розподілення бюджету обчислень та алгоритми градієнта знань.
Методологія поверхні реагування (RSM)
У методі Бокса-Вілсона (англ. Response surface methodology) мета полягає в тому, щоб знайти взаємозв'язок між вхідними змінними та змінними відгука. Процес починається зі спроби підігнати модель лінійної регресії. Якщо P-значення виявиться низьким, буде реалізована поліноміальна регресія вищого ступеня, яка є квадратичною. Процес пошуку гарного співвідношення між вхідними змінними та змінними відгуку буде виконуватися для кожного тесту моделювання. При оптимізації моделювання можна використовувати метод поверхні відгуку, щоб знайти найкращі вхідні змінні, які дають бажані результати з погляду змінних відгуків.[7]
Евристичні методи
Евристичні методи змінюють точність на швидкість. Їхня мета — знайти гарне рішення швидше, ніж традиційні методи, коли вони надто повільні або не можуть вирішити проблему. Зазвичай замість оптимального значення знаходять локальне оптимальне; однак значення вважаються досить близькими до остаточного рішення. Приклади таких методів є пошук табу та генетичні алгоритми.[4]
Метамоделі дозволяють дослідникам отримувати надійні наближені результати моделей без проведення дорогих та трудомістких комп'ютерних симуляцій. Отже, процес оптимізації моделі може зайняти менше часу та витрат на обчислення.[8]
Стохастичне наближення
Стохастична апроксимація використовується коли функція не може бути обчислена безпосередньо, лише оцінена за допомогою шумних спостережень. У цих сценаріях метод (або сімейство методів) шукає екстремуми цих функцій. Цільова функція буде:[9]
- є випадковою величиною, яка представляє шум;
- є параметром, який мінімізує ;
- є областю визначення параметра .
Методи оптимізації без похідних
Оптимізація без похідних застосовується до задачі оптимізації, коли її похідні відсутні або ненадійні. Методи, що не використовують похідні, створюють модель на основі значень вибіркових функцій або створюють вибірковий набір значень функцій без використання докладної моделі. Оскільки метод не використовує похідні, його не можна порівнювати з методами, заснованими на похідних.[10]
Для задач оптимізації без обмежень він має вигляд:
Обмеження оптимізації без похідних:
1. Деякі методи не можуть впоратися з завданнями оптимізації з більш ніж кількома змінними; результати зазвичай не такі точні. Тим не менш, існує безліч практичних випадків, коли методи без похідних були успішними у нетривіальних задачах оптимізації моделювання, які включають випадковість, що виявляється як «шум» у цільовій функції. Наприклад, [5][11].
2. Зіткнувшись із мінімізацією невипуклих функцій, він покаже свої обмеження.
3. Методи оптимізації без похідних відносно прості і легкі, але, як і для більшості методів оптимізації, при практичної реалізації (наприклад, при виборі параметрів алгоритму) потрібна певна обережність.
Динамічне програмування
Динамічне програмування має справу з ситуаціями, коли рішення ухвалюються поетапно. Ключ до вирішення таких проблем — знайти компроміс між поточними та майбутніми витратами.[12]
Одна динамічна базова модель має дві особливості:
1) Вона має дискретну динамічну систему за часом.
2) Функція вартості є адитивною з часом.
Для дискретних функцій динамічне програмування має вигляд:
- є індекс дискретного часу.
- це стан часу k, що містить інформацію минулого і готує її до майбутньої оптимізації.
- є контрольною змінною.
- є випадковим параметром.
Для функції вартості вона має вигляд:
це вартість у кінці процесу.
Так як вартість не може бути оптимізована суттєво, можна використовувати очікуване значення:
Нейродинамічне програмування
Нейродинамічне програмування аналогічне динамічному програмуванню, за винятком того, що перше має концепцію апроксимаційних архітектур. Метод поєднує в собі штучний інтелект, алгоритми на основі моделювання та методи функціонального підходу. «Нейро» в цьому терміні походить від спільноти штучного інтелекту. Це означає навчитися приймати покращені рішення на майбутнє за допомогою вбудованого механізму, що базується на поточній поведінці. Найважливіша частина нейродинамічного програмування — це побудова навченої нейромережі для вирішення оптимальної задачі.[13]
Обмеження
Оптимізація на основі моделювання має деякі обмеження, такі як складність створення моделі, яка імітує динамічну поведінку системи таким чином, який вважається досить добрим для її представлення. Інша проблема — складність визначення неконтрольованих параметрів як реальної системи, так і моделі. Більше того, можна отримати лише статистичну оцінку реальних значень. Визначити цільову функцію непросто, оскільки вона є результатом вимірювань, що впливає на розв'язки.[14][15]
Посилання
- Nguyen, Anh-Tuan, Sigrid Reiter, and Philippe Rigo. «A review on simulation-based optimization methods applied to building performance analysis.»Applied Energy 113 (2014): 1043—1058.
- Carson, Yolanda, and Anu Maria. «Simulation optimization: methods and applications.» Proceedings of the 29th Winter Simulation Conference. IEEE Computer Society, 1997.
- Jalali, Hamed, and Inneke Van Nieuwenhuyse. «Simulation optimization in inventory replenishment: a classification.» IIE Transactions 47.11 (2015): 1217—1235.
- Abhijit Gosavi, Simulation‐Based Optimization: Parametric Optimization Techniques and Reinforcement Learning, Springer, 2nd Edition (2015)
- Fu, Michael, editor (2015). Handbook of Simulation Optimization. Springer.
- Spall, J.C. (2003). Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control. Hoboken: Wiley.
- Rahimi Mazrae Shahi, M., Fallah Mehdipour, E. and Amiri, M. (2016), Optimization using simulation and response surface methodology with an application on subway train scheduling. Intl. Trans. in Op. Res., 23: 797—811. DOI:10.1111/itor.12150
- Yousefi, Milad; Yousefi, Moslem; Ferreira, Ricardo Poley Martins; Kim, Joong Hoon; Fogliatto, Flavio S. (2018). Chaotic genetic algorithm and Adaboost ensemble metamodeling approach for optimum resource planning in emergency departments. Artificial Intelligence in Medicine 84: 23–33. PMID 29054572. doi:10.1016/j.artmed.2017.10.002.
- Powell, W. (2011). Approximate Dynamic Programming Solving the Curses of Dimensionality (2nd ed., Wiley Series in Probability and Statistics). Hoboken: Wiley.
- Conn, A. R.; Scheinberg, K.; Vicente, L. N. (2009). Introduction to Derivative-Free Optimization. MPS-SIAM Book Series on Optimization. Philadelphia: SIAM. Retrieved 2014-01-18.
- Fu, M.C., Hill, S.D. Optimization of discrete event systems via simultaneous perturbation stochastic approximation. IIE Transactions 29, 233—243 (1997). https://doi.org/10.1023/A:1018523313043
- Cooper, Leon; Cooper, Mary W. Introduction to dynamic programming. New York: Pergamon Press, 1981
- Van Roy, B., Bertsekas, D., Lee, Y., & Tsitsiklis, J. (1997). Neuro-dynamic programming approach to retailer inventory management. Proceedings of the IEEE Conference on Decision and Control, 4, 4052-4057.
- Prasetio, Y. (2005). Simulation-based optimization for complex stochastic systems. University of Washington.
- Deng, G., & Ferris, Michael. (2007). Simulation-based Optimization, ProQuest Dissertations and Theses