Поліноміальна регресія

Поліноміальні регресійні моделі, як правило, налаштовують за допомогою методу найменших квадратів. Метод найменших квадратів мінімізує дисперсію незміщених оцінок коефіцієнтів за умов теореми Гаусса-Маркова. Метод найменших квадратів був опублікований в 1805 році Лежандром і в 1809 році Гауссом. Перший опис експерименту для поліноміальної регресії з'явився в 1815 році у статті Жергонна.[2][3] У ХХ столітті поліноміальна регресія відіграла важливу роль у розвитку регресійного аналізу, з більшим акцентом на питаннях Планування експерименту та статистичному висновуванні.[4] Зовсім недавно використання поліноміальних моделей було доповнено іншими методами, причому неполіноміальні моделі мають переваги для деяких класів задач.^{[джерело?]}

Кубічна поліноміальна регресія, допасована до зімітованого набору даних. Довірча смуга є одночасно 95 %-вою довірчою смугою, побудованою з використанням підходу Шеффе.

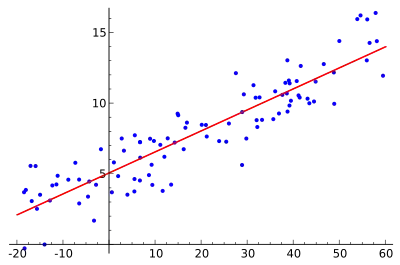
Метою регресійного аналізу є моделювання очікуваного значення залежної змінної y через значення незалежної змінної (або вектора незалежних змінних) x. У простій лінійній регресії використовується модель

${\displaystyle y=\beta _{0}+\beta _{1}x+\varepsilon ,\,}$

де ε невизначена випадкова помилка із середнім нулем, обумовленим скалярною змінною x. У цій моделі для кожної одиниці збільшення значення x, умовне сподівання y збільшується на β₁ одиниць.

У багатьох умовах такий лінійний зв'язок може не мати місце. Наприклад, якщо ми моделюємо вихід хімічного синтезу з точки зору температури, при якій відбувається синтез, ми можемо виявити, що вихід поліпшується за рахунок збільшення кількості для кожної одиниці підвищення температури. У цьому випадку ми можемо запропонувати квадратичну модель форми

${\displaystyle y=\beta _{0}+\beta _{1}x+\beta _{2}x^{2}+\varepsilon .\,}$

У цій моделі при підвищенні температури від x до x + 1 одиниць очікуваний вихід змінюється на ${\displaystyle \beta _{1}+\beta _{2}(2x+1).}$ (Це можна побачити, замінивши x у цьому рівнянні на x+1 і віднявши рівняння з x з рівняння з x+1.) Для нескінченно малих змін x, вплив на y дається повною похідною по x: ${\displaystyle \beta _{1}+2\beta _{2}x.}$. Той факт, що зміна результату залежить від x є тим, що робить зв'язок між x та y нелінійним, навіть незважаючи на те, що модель є лінійною за параметрами, що підлягають оцінці.

Загалом, ми можемо змоделювати очікуване значення y як поліном ступеню n, отримуючи загальну модель поліноміальної регресії

${\displaystyle y=\beta _{0}+\beta _{1}x+\beta _{2}x^{2}+\beta _{3}x^{3}+\cdots +\beta _{n}x^{n}+\varepsilon .\,}$

Зручно, всі ці моделі є лінійними з точки зору оцінки, оскільки функція регресії є лінійною з точки зору невідомих параметрів β₀, β₁, …. Таким чином, для аналізу методом найменших квадратів, обчислювальні та виведені задачі поліноміальної регресії можут бути повністю вирішені за допомогою методів лінійної регресії. Це робиться шляхом обробки x, x², … як окремих незалежних змінних у моделі множинної регресії.

Модель поліноміальної регресії

${\displaystyle y_{i}\,=\,\beta _{0}+\beta _{1}x_{i}+\beta _{2}x_{i}^{2}+\cdots +\beta _{m}x_{i}^{m}+\varepsilon _{i}\ (i=1,2,\dots ,n)}$

може бути виражена у матричній формі через матрицю проектування ${\displaystyle \mathbf {X} }$, вектор відповіді ${\displaystyle {\vec {y}}}$, вектор параметрів ${\displaystyle {\vec {\beta }}}$ та вектор ${\displaystyle {\vec {\varepsilon }}}$ випадкових помилок. I-тий рядок ${\displaystyle \mathbf {X} }$ and ${\displaystyle {\vec {y}}}$ міститиме значення x та y для i-го рядка вибірки даних. Тоді модель можна записати як систему лінійних рівнянь:

${\displaystyle {\begin{bmatrix}y_{1}\\y_{2}\\y_{3}\\\vdots \\y_{n}\end{bmatrix}}={\begin{bmatrix}1&x_{1}&x_{1}^{2}&\dots &x_{1}^{m}\\1&x_{2}&x_{2}^{2}&\dots &x_{2}^{m}\\1&x_{3}&x_{3}^{2}&\dots &x_{3}^{m}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&x_{n}&x_{n}^{2}&\dots &x_{n}^{m}\end{bmatrix}}{\begin{bmatrix}\beta _{0}\\\beta _{1}\\\beta _{2}\\\vdots \\\beta _{m}\end{bmatrix}}+{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\vdots \\\varepsilon _{n}\end{bmatrix}},}$

що при використанні чисто матричної нотації записується як

${\displaystyle {\vec {y}}=\mathbf {X} {\vec {\beta }}+{\vec {\varepsilon }}.\,}$

Вектор розрахункових коефіцієнтів поліноміальної регресії (за допомогою оцінки звичайних найменших квадратів) становить

${\displaystyle {\widehat {\vec {\beta }}}=(\mathbf {X} ^{\mathsf {T}}\mathbf {X} )^{-1}\;\mathbf {X} ^{\mathsf {T}}{\vec {y}},\,}$

припускаючи m < n щоб матриця була оборотною, оскільки ${\displaystyle \mathbf {X} }$ є визначником Вандермонда, умова оберненості гарантовано буде виконуватися, якщо всі значення ${\displaystyle x_{i}}$ різні. Це унікальне рішення методом найменших квадратів.

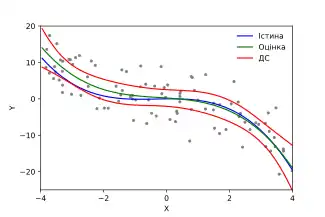
Хоча поліноміальна регресія технічно є приватним випадком багаторазової лінійної регресії, інтерпретація налаштованої моделі поліноміальної регресії вимагає дещо іншої перспективи. Часто буває важко інтерпретувати окремі коефіцієнти в поліноміальній регресії, оскільки основні одночлени можуть бути високо корельованими. Наприклад, x та x² мають кореляцію близько 0.97 коли x рівномірно розподіляється на інтервалі (0, 1). Хоча кореляцію можна зменшити за допомогою ортогональних поліномів, загалом більш інформативно розглядати налаштовану функцію регресії в цілому. Поточкові або одночасні довірчі смуги потім можуть бути використані для забеспечення відчуття невизначеності в оцінці функції регресії.

Поліноміальна регресія є одним із прикладів регресійного аналізу з використанням базисних функцій для моделювання функціональної залежності між двома величинами. Більш конкретно, вона замінює ${\displaystyle x\in \mathbb {R} ^{d_{x}}}$ в лінійній регресії з поліноміальною основою ${\displaystyle \varphi (x)\in \mathbb {R} ^{d_{\varphi }}}$, наприклад, ${\displaystyle [1,x]{\mathbin {\stackrel {\varphi }{\rightarrow }}}[1,x,x^{2},\ldots ,x^{d}]}$. Недоліком поліноміальних основ є те, що базисні функції є «нелокальними», тобто налаштоване значення y при заданому значенні x = x₀ сильно залежить від значень даних з x далеких від x₀.[5] У сучасній статистиці поліноміальні базисні функції використовуються поряд з новими базисними функціями, такими як сплайни, радіальна базисні функції та вейвлети. Ці сімейства базисних функцій пропонують більш ощадливу налаштованість багатьом типам даних.

Метою поліноміальної регресії є моделювання нелінійної залежності між незалежними та залежними змінними (технічно, між незалежною змінною та умовним середнім значенням залежної змінної). Це схоже на мету непараметричної регресії, яка спрямована на охоплення нелінійних відношень регресії. Тому непараметричні підходи до регресії, такі як згладжування можуть бути корисними альтернативами поліноміальної регресії. Деякі з цих методів використовують локалізовану форму класичної поліноміальної регресі.[6] Перевага традиційної поліноміальної регресії полягає в тому, що можна використовувати вивідну структуру множинної регресії (це також має місце при використанні інших сімейств базисних функцій, таких як сплайни).

Кінцевою альтернативою є використання ядрових моделей таких як метод опорних векторів з поліноміальним ядром.

Якщо залишки мають неоднакову дисперсію, тоді для оцінки може бути використаний метод зважених найменших квадратів.[7]

• Допасовування кривої
• Лінійна регресія
• Локальна поліноміальна регресія
• Поліноміальне та раціональне моделювання функцій
• Поліноміальна інтерполяція
• Метод Бокса — Вілсона
• Згладжуючий сплайн

• Microsoft Excel використовує поліноміальну регресію при підборі лінії тренду до точок даних на графіку розсіювання XY.[8]