Ортогональна траєкторія
Ортогональні траєкторії — лінії, що перетинають задане сімейство кривих під прямим кутом. Якщо — кутовий коефіцієнт дотичної до ортогональної траєкторії, а — кутовий коефіцієнт дотичної до кривої даного сімейства, то і повинні в кожній точці відповідати умові ортогональності:
Нехай у нас є сімейство кривих , де — константа. Тоді ортогональні траєкторії можуть бути знайдені шляхом розв'язку системи диференціальних рівнянь:
Використовуючи визначення градієнта, можна записати:
Таким чином:
Приклади
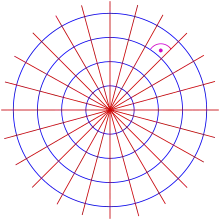
Нехай у нас є сімейство прямих ліній, що проходять через початок координат, заданих рівнянням . Диференціюючи дане рівняння по змінній , отримуємо:
Виключимо параметр із системи:
Замінимо на :
Ми отримали своєрідне диференціальне рівняння з перемінними. Інтегруючи, отримуємо:
Дане рівняння є ніщо інше, як рівняння кола радіуса . Дійсно:
Література
Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. (стор. 23, Приклад 8)
Посилання
- Ортогональні траєкторії(рос.)
