Площина Мебіуса
Площина Мебіуса (також колова площина і інверсна площина) — площина, описувана системою аксіом ідентичності, в якій основну роль відіграють точки і так звані узагальнені кола.
Прикладом колової площини є евклідова площина, доповнена однією ідеальною точкою (). Узагальненими колами є звичайні кола, а також звичайні прямі, доповнені точкою , відношення інцидентності — відношення належності.
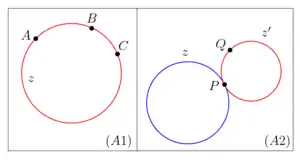
Колова площина: аксіоми (A1), (A2)
Визначення
Колова площина це структура інцидентності , де — множина точок, — множина узагальнених кіл і — симетричне відношення інцидентності між і , яка задовольняє таким аксіомам:
- A1: Для будь-яких трьох точок існує рівно одне узагальнене коло , яке інцидентне .
- A2: Для будь-якого узагальненого кола , будь-яких точок і існує рівно одне узагальнене коло , таке, що: і (тобто, і дотикаються одне з одним у точці ).
- А3: Будь-яке узагальнене коло інцидентне принаймні трьом точкам. Існує щонайменше чотири різні точки, які не інцидентні одному колу.
Див. також
Посилання
- EF Assmus Jr and JD Key, Designs and their codes, Cambridge University Press, ISBN 0-521-45839-0. с. 309—312.
- P. Dembowski, Finite geometries, Springer Verlag, 1968, repr.1996, ISBN 3540617868.
- DR Hughes and FC Piper, Design theory, Cambridge University Press, ISBN 0-521-35872-8. с. 133—136.
- И. М. Виноградов. Мёбиуса плоскость // Математическая энциклопедия. — М. : Советская энциклопедия, 1977—1985. — стаття з математичної енциклопедії. В. В. Афанасьєв.
- Möbius plane — стаття з Encyclopaedia of Mathematics.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.