Сфера Рімана
Сфера Рімана — ріманова поверхня, природна структура на розширеній комплексній площині яка є комплексною проективною прямою Іншими словами це модель розширеної комплексної площини, де до звичайної комплексної площини додається точка на нескінченності. Відповідно до моделі Рімана, точка «∞» наближається до дуже великих чисел, так само як точка «0» є близькою до дуже малих чисел.
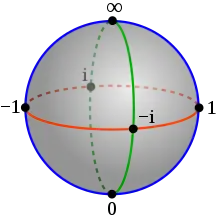
Як дійсний многовид дифеоморфна двовимірній сфері
Координати
Числові координати на сфері Рімана вводяться трьома способами:
- афінна комплексна координата z, яка приймає значення ;
- проективні комплексні координати ;
- тривимірні дійсні координати , пов'язані рівнянням:
- .
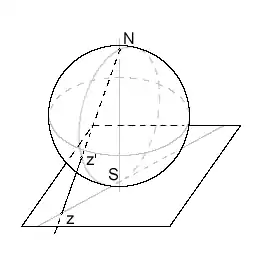
Перехід від одних координат до інших задається формулами:
задає відображення сфери з виколотим полюсом на комплексну площину, яке називається стереографічною проекцією.
Перетворення Мебіуса
Автоморфізмами сфери Рімана є перетворення Мебіуса. Нехай — матриця із . Її дія на сфері Рімана в термінах проективних комплексних координат — просто множення вектора-стовпця координат на матрицю. В афінних координатах дія виглядає так:
Додаток
Сфера Рімана відома в теоретичній фізиці.
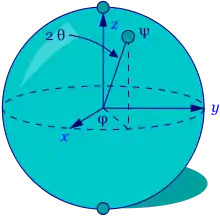
В спеціальній теорії відносності сфера Рімана є моделлю небесної сфери. Перетворення Мебіуса пов'язані з перетвореннями Лоренца. Перетворення Мебіуса і Лоренца зв'язані також зі спінорами. В квантовій механіці сфера Рімана параметризує стани систем, описуваних 2-вимірним простором (див. q-біт), зокрема спіна масивних часток з спіном 1/2, таких як електрон. В цьому контексті сферу Рімана називають сферою Блоха і використовують на ній координати «широта-довгота» майже як на звичайній сфері, тільки широту відраховують від полюса і ділять кут на 2, т. ч. (див. мал.)
В такому випадку вірні співвідношення: