Подвійний маятник
У фізиці і математиці, у галузі динамічних систем, подвійний маятник це маятник з іншим маятником прикріпленим до його кінця, і є простою фізичною системою, яка проявляє різноманітну динамічну поведінку зі значною залежністю від початкових умов.[1] Рух маятника керується пов'язаними звичайними диференціальними рівняннями. Для деяких енергій його рух є хаотичним.

Аналіз
Можна розглядати декілька варіантів подвійних маятників; два члени можуть бути однакові чи різні завдовжки та за вагою, вони можуть бути простими маятниками або фізичними маятниками і рух може бути у трьох вимірах або обмежений вертикальною площиною. В наступному аналізі, члени обрані як однакові фізичні маятники довжини і маси , і рух обмежений двома вимірами.
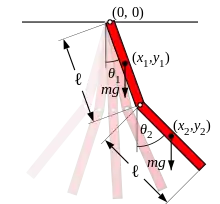
У фізичного маятника, маса розподілена вздовж усієї його довжини. Якщо маса розподілена рівномірно, тоді центр мас кожного члена збігається з його геометричним центром, і член має такий момент інерції щодо цієї точки.
Це зручно використовувати кути між кожним членом і вертикаллю як узагальнені координати визначаючи простір конфігурацій системи. Якщо покласти початок координат декартової системи координат у точці підвішування першого маятника, тоді центр мас цього маятника перебуває в:
і центр мас другого в
Цієї інформації достатньо, щоб записати Лагранжіан.
Лагранжіан
Лагранжіан є різницею між кінетичною енергією і потенціальною енергією:
Перший доданок це лінійна кінетична енергія центру мас тіл і другий доданок це обертова кінетична енергія центрів мас кожного стрижня. Останній доданок це потенціальна енергія тіл у однорідному гравітаційному полі.
Підставляючи координати і перегруповуючи рівняння маємо



Тут відбувається збереження лише однієї величини (енергії), і не збережений узагальнений імпульс. Два імпульси можна записати як
і
Ці вирази можна обернути, щоб отримати
і
Решта рівнянь руху можна записати як
і
Останні чотири рівняння є явними формулами для часової еволюції системи із заданим поточним станом. Це не виявляється можливим просунутись далі і інтегрувати ці рівняння аналітично, щоб отримати формули для θ1 і θ2 як функції від часу. Однак, можливо виконати числове інтегрування використовуючи метод Рунге — Кутти або подібну техніку.
Примітки
- Levien RB and Tan SM. Double Pendulum: An experiment in chaos.American Journal of Physics 1993; 61 (11): 1038