Полілогарифм

Полілогарифм — спеціальна функція, що позначається ${\displaystyle \operatorname {Li} _{s}(z)}$ і визначається як нескінченний степеневий ряд

${\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}},}$

де s і z — комплексні числа, причому ${\displaystyle |z|<1}$. Для інших z робиться узагальнення за допомогою аналітичного продовження.

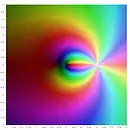
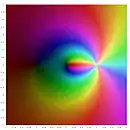
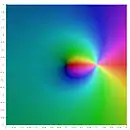
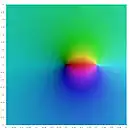
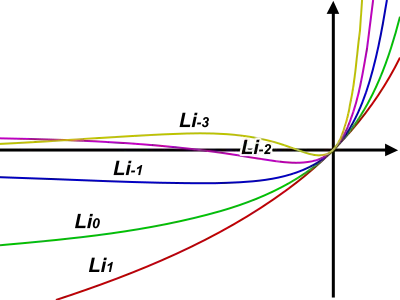
Частковим випадком є ${\displaystyle s=1}$, за якого ${\displaystyle \operatorname {Li} _{1}(z)=-\ln(1-z)}$. Функції ${\displaystyle \operatorname {Li} _{2}(z)}$ і ${\displaystyle \operatorname {Li} _{3}(z)}$ отримали назви дилогарифма і трилогарифма відповідно. Для полілогарифмів різних порядків виконується співвідношення

${\displaystyle \operatorname {Li} _{s+1}(z)=\int _{0}^{z}{\frac {\operatorname {Li} _{s}(t)}{t}}\,\mathrm {d} t.}$

Альтернативними визначеннями полілогарифма є інтеграли Фермі — Дірака і Бозе — Ейнштейна.