Популяційна динаміка

• Закон Мальтуса
• Модель Леслі
• Модель Лотки-Вольтера (хижак-жертва)

Рис. 1. Експоненціальне зростання гіпотетичної популяції одноклітинного організму, що ділиться кожні 4 год.: а — арифметична шкала, б — логарифмічна шкала

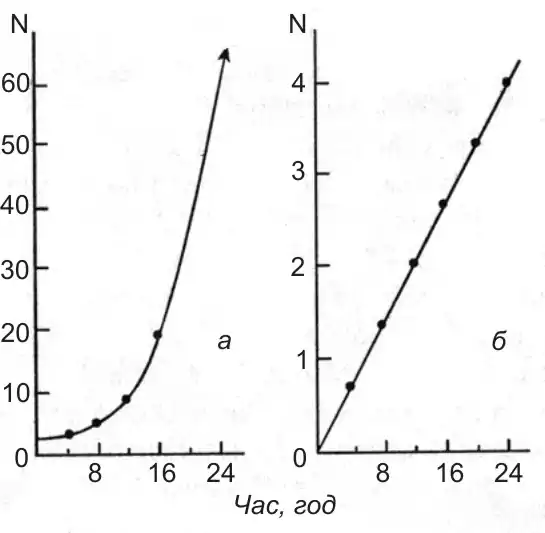
Ще в XVII ст. було встановлено, що чисельність популяцій зростає за законом геометричної прогресії, а вже в кінці XVIII ст. Томас Мальтус (1766—1834) висунув свою відому теорію про зростання народонаселення в геометричній прогресії. Ця закономірність зростання виражається кривою, зображеною на рис. 1.

Сучасною математичною мовою ця крива відображає експоненційний ріст чисельності організмів і описується рівнянням:

де:

• N_t — чисельність популяції в момент часу t;
• N₀ — чисельність популяції в початковий момент часу t₀;
• е — основа натурального логарифма (2,7182...);
• r — показник, що характеризує темп розмноження особин в даній популяції.

Експоненційне зростання можливе тільки тоді, коли r має постійне чисельне значення, так як швидкість росту популяції пропорційна самій чисельності.

Якщо чисельність відкласти в логарифмічному масштабі, то крива набуває вигляду прямої лінії (рис. 2, б). Таким чином, експоненційний ріст чисельності популяції — це зростання чисельності її особин в незмінних умовах. Умови, що зберігаються тривалий час постійними, неможливі в природі. Якби це було не так, то, наприклад, звичайні бактерії могли б дати таку масу органічної речовини, яка могла б покрити всю земну кулю шаром завтовшки в 2 метри за 2 години. Однак такого в природі не відбувається, тому що існує безліч обмежуючих факторів. Але є приклади, коли при уповільненні зростання, тобто при зниженні r, експоненційний ріст зберігається, він може виникати і на коротких відрізках життя популяцій.

Рис. 2. Логістична модель зростання популяції: а — крива зростання чисельності (N), б — залежність питомої швидкості росту (г) від чисельності (N), в — залежність народжуваності (b) та смертності (d) від чисельності; К — гранична чисельність

Рис. 3

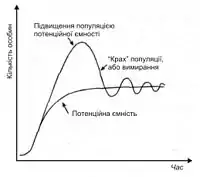
На рис. 3 показано, що J-подібна крива росту чисельності популяції перетворюється на S-подібну при обмежуючому впливі лімітуючих факторів (за: Міллер, 1993).

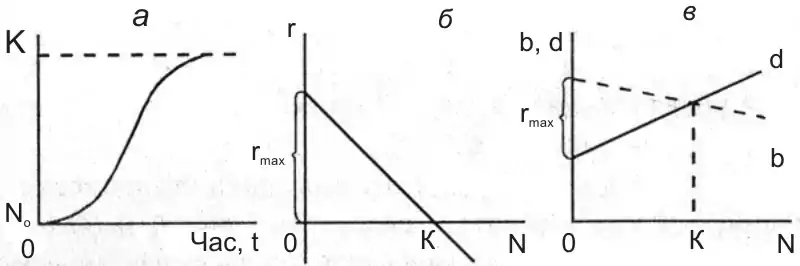
Для опису S-подібного зростання може бути використано чимало різних рівнянь, але найбільшу популярність отримало найпростіше з них — так зване логістичне.

Вперше запропоноване як модель зростання народонаселення в 1838 р. бельгійським математиком П. Ф. Ферхюльстом (Ферхюльст, 1838), воно було перевідкрито заново американськими дослідниками Р. Перлом і Л. Рідом (Pearl, Reed, 1920) в 1920 р., які, втім, уже через рік визнали пріоритет Ферхюльста. В основі логістичної моделі лежить дуже просте припущення, а саме лінійне зниження швидкості питомого зростання r = dN/Ndt в міру зростання чисельності N, причому швидкість ця стає рівною нулю при досягненні певної граничної для даного середовища чисельності К. Отже, якщо N = К, то ra = 0. У популярних підручниках екології іноді не зовсім вірно постійний коефіцієнт з логістичного рівняння rmax прирівнюють до показника будь-якого експоненціального зростання даної популяції, тобто стверджується, що rmax = ra. Насправді це не так: для дотримання експоненціального зростання необхідно, щоб показник ra був постійною величиною (r = const), для здійснення же логістичного зростання необхідно, щоб показник ra знижувався по лінійному закону при збільшенні чисельності N. Нагадаємо, що ra як у рівнянні експоненційному, так і в рівнянні логістичному дорівнює різниці питомої народжуваності і питомої смертності. При логістичному зростанні ra майже дорівнює rmax тільки при чисельності, близькій до нуля, тобто тоді, коли народжуваність b максимальна, а смертність мінімальна d. Лінійний характер зміни ra при збільшенні N передбачає лінійні зміні, як народжуваності, так і смертності.

Багато екологів 1920-30-х рр., особливо ті, що мали справу з лабораторними культурами організмів, поставилися з великим ентузіазмом до використання логістичного рівняння для опису експериментальних даних. Ентузіазм цей пояснювався, мабуть, тим, що S-подібне (в широкому сенсі цього слова) зростання популяцій дійсно спостерігалося дуже часто, а логістичне рівняння, наскільки б не було воно недосконалим, описувало це зростання і, таким чином, служило першою моделлю динаміки чисельності, що дозволяє говорити про загальні закономірності цього процесу.

• Популяційні хвилі

• Вибух популяційний // Словник-довідник з екології : навч.-метод. посіб. / уклад. О. Г. Лановенко, О. О. Остапішина. — Херсон : ПП Вишемирський В. С., 2013. — С. 34.
• Динаміка популяцій // Словник-довідник з екології : навч.-метод. посіб. / уклад. О. Г. Лановенко, О. О. Остапішина. — Херсон : ПП Вишемирський В. С., 2013. — С. 68.
• Г.Г. ЖИЛЯЄВ СУБПОПУЛЯЦІЙНА ТА ПОПУЛЯЦІЙНА ДИНАМІКА