Псевдосфера

Псевдосфера (від «псевдо»… і грецького — куля) — поверхня сталої від'ємної кривини. Утворена обертанням трактриси навколо її асимптоти. Для достатньо малих частин псевдосфери, які не мають особливих точок, справедливими є співвідношення геометрії Лобачевського. Це відкриття Еудженіо Бельтрамі у 1868 відіграло важливу роль у розвитку неевклідових геометрій, бо дало змогу переконатись у реальності геометрії Лобачевського. Назва несправжня сфера підкреслює схожість і відмінність між псевдосферою і сферою - у сфери поверхня має сталу додатну кривину.

Напів-псевдосфера

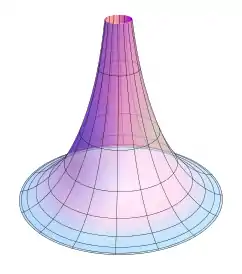
Теоретична псевдосфера

У загальній інтерпретації, псевдосфера радіусу R — це будь-яка поверхня кривини −1/R², за аналогією зі сферою радіусу R, для якої поверхня кривини є 1/R².

Термін був запропонований Еудженіо Бельтрамі у його праці 1868 року про моделі геометрії Лобачевського.[1]

Трактрисоїд

Трактрисоїд

Термін також використовують до певної поверхні, яка має назву трактрисоїд і є результатом обертання трактриси довкола її асимптоти. Наприклад, напів-псевдосфера (з радіусом 1) є поверхнею обертання трактриси, обмеженої параметрами[2]:

t\mapsto \left(t-\tanh {t},\operatorname {sech} \,{t}\right),\quad \quad 0\leq t<\infty .

Ще 1693 року Християн Гюйгенс з'ясував, що об'єм та площа поверхні псевдосфери є скінченними[3], незважаючи на нескінченність протяжності поверхні вздовж осі обертання. Для заданого радіусу R, площа поверхні буде 4πR², так само як і для сфери, а об'єм дорівнює $23$ πR³, тобто половині сфери з таким самим радіусом[4][5].

Примітки

Beltrami, Eugenio (1868). Saggio sulla interpretazione della geometria non euclidea. Gior. Mat. (Italian) 6: 248–312.
(Також Beltrami, Eugenio. Opere Matematiche (Italian) 1. с. 374–405. ISBN 1-4181-8434-9.;
Beltrami, Eugenio (1869). Essai d'interprétation de la géométrie noneuclidéenne. Annales de l'École Normale Supérieure (French) 6: 251–288.)
Bonahon, Francis (2009). Low-dimensional geometry: from Euclidean surfaces to hyperbolic knots. AMS Bookstore. с. 108. ISBN 0-8218-4816-X., Chapter 5, page 108
Mangasarian, Olvi L.; Pang, Jong-Shi (1999). Computational optimization: a tribute to Olvi Mangasarian, Volume 1. Springer. с. 324. ISBN 0-7923-8480-6., Chapter 17, page 324
Le Lionnais, F. (2004). Great Currents of Mathematical Thought, Vol. II: Mathematics in the Arts and Sciences (вид. 2). Courier Dover Publications. с. 154. ISBN 0-486-49579-5., Chapter 40, page 154
Weisstein, Eric W. Pseudosphere(англ.) на сайті Wolfram MathWorld.

Джерела

Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Beltrami, Eugenio (1868). Saggio sulla interpretazione della geometria non euclidea. Gior. Mat. (Italian) 6: 248–312.
(Також Beltrami, Eugenio. Opere Matematiche (Italian) 1. с. 374–405. ISBN 1-4181-8434-9.;
Beltrami, Eugenio (1869). Essai d'interprétation de la géométrie noneuclidéenne. Annales de l'École Normale Supérieure (French) 6: 251–288.)

[2] Bonahon, Francis (2009). Low-dimensional geometry: from Euclidean surfaces to hyperbolic knots. AMS Bookstore. с. 108. ISBN 0-8218-4816-X., Chapter 5, page 108

[3] Mangasarian, Olvi L.; Pang, Jong-Shi (1999). Computational optimization: a tribute to Olvi Mangasarian, Volume 1. Springer. с. 324. ISBN 0-7923-8480-6., Chapter 17, page 324

[4] Le Lionnais, F. (2004). Great Currents of Mathematical Thought, Vol. II: Mathematics in the Arts and Sciences (вид. 2). Courier Dover Publications. с. 154. ISBN 0-486-49579-5., Chapter 40, page 154

[5] Weisstein, Eric W. Pseudosphere(англ.) на сайті Wolfram MathWorld.