Трактриса
Трактриса (від лат. trahere — тягнути) крива, по якій рухається об'єкт, коли його тягнути по горизонтальній площині за мотузку фіксованої довжини, якщо напрямок руху тягача є ортогональним до початкового положення мотузки та швидкість тягача нескінченно мала величина. Тому трактриса буде кривою погоні.
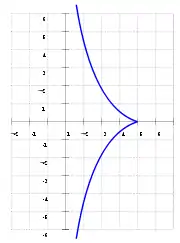
З геометричної точки зору трактрису визначають як трансцендентну криву, для якої довжина відрізка дотичної від точки дотику до точки перетину з фіксованою прямою є постійною величиною.
Ця крива була вперше запроваджена Клодом Перро в 1670, а потім вивчалась Ісааком Ньютоном (1676) і Християном Гюйгенсом (1692).
Рівняння трактриси

Припустимо, об'єкт розташовано в точці (a,0) (або (4,0) як на малюнку, наведеному вище), а тягач знаходиться в початку координат, тоді довжиною мотузки a (4 на малюнку). Тягач починає рухатися уздовж осі y в додатному напрямку. У кожний момент руху мотузка буде дотичною до кривої y = y (x) описаного об'єкта, так що крива повністю визначається рухом тягача. Математично рух можна описати за допомогою диференціального рівняння:
з початковою умовою y (a) = 0, розв'язком якого є
Перша частина цього рішення також може бути записана, як
де arsech є оберненою гіперболічною функцією ареакосеканс.
Від'ємна гілка відповідає випадку, коли тягач переміщується у від'ємному напрямку від початку координат. Обидві гілки належать до трактриси та зустрічаються в особливій точці (a, 0).
Параметричний опис:
Визначення трактриси
Важливою ознакою трактриси є постійність відстані між точкою P на кривій та перетином дотичної в Р з асимптотою кривої.
Трактриса може бути розглянута в різні способи:
- Це геометричне місце точок центру гіперболічної спіралі при її розмотці (без ковзання) на прямій.
- Евольвента ланцюгової лінії, яка описує повністю гнучку, нееластичну, однорідну струну, прикріплену до двох точок, яку помістили у гравітаційне поле. Ланцюгова лінія задається рівнянням .
- Траєкторія, яка визначається серединою заднього моста автомобіля, який тягне канат з постійною швидкістю і в постійному напрямку (на початку руху перпендикулярного до автомобіля).
Функція має горизонтальні асимптоти. Крива симетрична щодо осі Y. Радіус кривини .
Поверхня обертання трактриси навколо своєї асимптоти (осі x), є псевдосферою. У 1868 році Еудженіо Бельтрамі вивчав псевдосферу, як поверхню постійної від'ємної гаусової кривини. Псевдосфера є локальною моделлю неевклідової геометрії. Ця ідея була здійснена Едвардом Казнером та Джеймсом Ньюменом у книзі «Математика та Уява», де вони показали іграшковий потяг, який перетягували за допомогою кишенькового годинника для створення трактриси.
Властивості трактриси
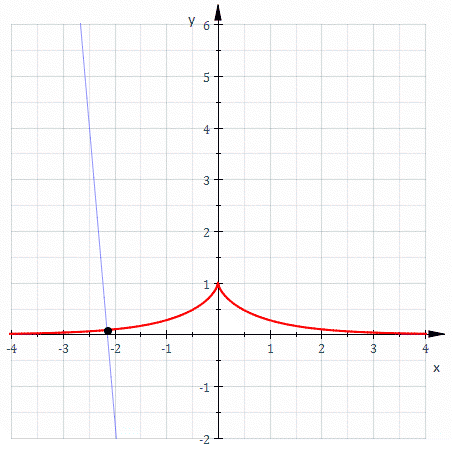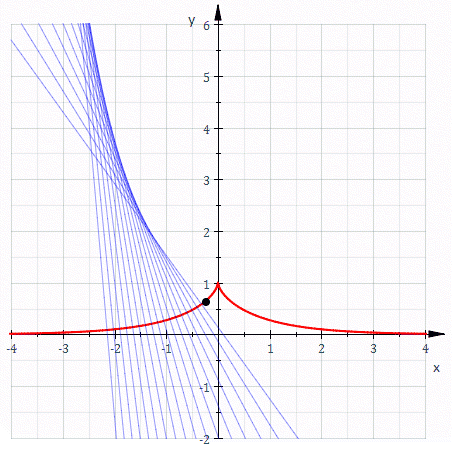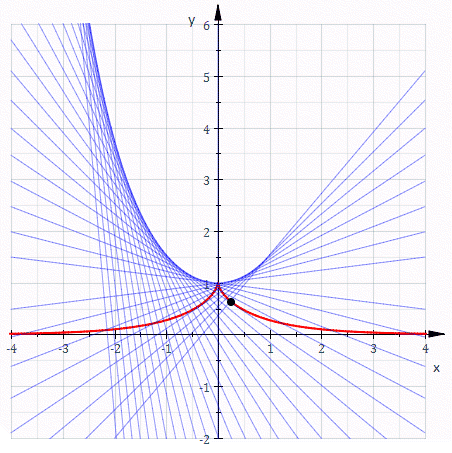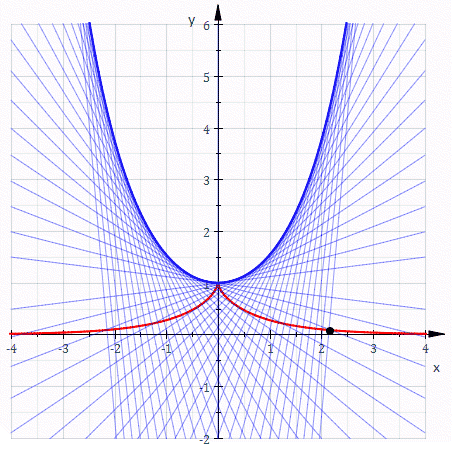
Площа, обмежена трактрисою і її асимптотою:
Довжина дуги, від точки (0 ; а) до довільної точки трактриси:
Радіус кривини:
Практичне застосування
В 1927 році була запатентована розробка — рупорний гучномовець, який заснований на припущенні, що фронт хвилі, яка проходить через рупор має сферичну форму з постійним радіусом. Ідея полягає в тому, щоб звести до мінімуму спотворення, викликані внутрішнім відбиттям звуку в рупорі. Отримана форма є поверхнею обертання трактриси.[1]
Обчислювальні машини
- В жовтні та листопаді 1692 року Християн Гюйгенс описав три трактриси створені машинами.
- В 1693 році Лейбніц оприлюднив машину, яка, в теорії, може інтегрувати будь-яке диференціальне рівняння. Машина була тягової конструкції.
- В 1706 році Джон Перкі побудував тягову машину для того, щоб реалізувати гіперболічну квадратуру.
- В 1729 році Джованні Полені побудував тяговий пристрій, що дозволив накреслити логарифмічні функції.
Посилання
- Едвард Казнер і Джеймс Ньюмен (1940) Математика і Уява, стор. 141–143.
- J. Денніс Лоуренс (1972). Каталог спеціальних плоских кривих. Dover Publications. с. 5, 199. ISBN 0-486-60288-5.
- Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Tractrix в архіві MacTutor (англ.)
- Tractrix на PlanetMath
- Famous curves on the plane. на PlanetMath
- Tractrix на MathWorld
- ЗДР карманного годинника Лейбніца на PHASER