Птолемеїв граф
У теорії графів птолеме́їв граф — це неорієнтований граф, у якому відстані по найкоротшому шляху задовольняють нерівності Птолемея (грецького астронома і математика Птолемея). Птолемеєві графи — це точно графи, які одночасно є і хордальними, і дистанційно-успадковуваними. Ці графи включають блокові графи [1] і є підкласом досконалих графів.

Птолемеїв граф
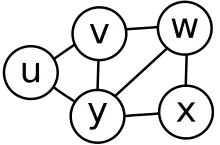
Граф-смарагд (або 3-віяло) не Птолемеїв

Блоковий граф, різновид птолемеєвих графів
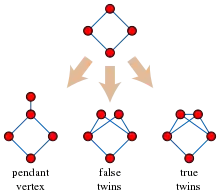
Три операції, за допомогою яких можна побудувати будь-який дистанційно-успадковуваний граф. Для птолемеєвих графів сусіди двійнят мають утворювати кліку, щоб запобігти побудові 4-циклу, показаного тут.
Опис
Граф є птолемеєвим тоді і тільки тоді, коли він задовольняє таким еквівалентним умовам:
- Відстані по найкоротшому шляху задовольняють нерівності Птолемея — для будь-яких чотирьох вершин u, v, w і x виконується нерівність d(u,v)d(w,x) + d(u,x)d(v,w) ≥ d(u,w)d(v,x) [1]. Наприклад, граф-смарагд (3-віяло) на малюнку не є птолемеєвим, оскільки в цьому графі d(u,w)d(v,x) = 4 більше, ніж d(u,v)d(w,x) + d(u,x)d(v,w) = 3
- Для будь-яких перекривних максимальних клік їх перетин є сепаратором, який розділяє різницю цих двох клік[2]. Для графу-смарагду на малюнку це не так: кліки uvy і wxy не розділяються їх перетином y оскільки існує ребро vw що з'єднує кліки.
- Будь-який цикл з k вершинами має щонайменше 3(k − 3)/2 діагоналей[2].
- Граф є і хордальним (будь-який цикл з довжиною, що перевищує три, має діагональ), і дистанційно-успадковуваним (будь-який зв'язний породжений підграф має ті ж відстані, що й весь граф)[2]. Граф-смарагд є хордальним, але не дистанційно-успадковуваним: у підграфі, породженому uvwx відстань від u до x дорівнює 3, що більше, ніж відстань між тими ж вершинами в повному графі. Оскільки як хордальні, так і дистанційно-успадковувані графи є досконалими, такими ж є і птолемеєві графи.
- Граф хордальний і не містить смарагдів — графів, утворених доданням двох неперетинних діагоналей у п'ятикутник[3].
- Граф є дистанційно-успадковуваним і не містить породжених 4-циклів[4].
- Граф можна побудувати з єдиної вершини послідовністю операцій, при яких додається нова вершина степеня 1 (висяча вершина) або дублюється наявна вершина (утворюючи близнюків або двійнят), з умовою, що операція подвоєння, в якій дублікат вершини не суміжний своїй парі (двійнята), тільки якщо сусіди цих подвоєних вершин утворюють кліку. Ці три операції, якщо не застосовувати зазначеної умови, утворюють всі дистанційно-успадковувані графи. Для утворення птолемеєвих графів недостатньо використовувати утворення висячих вершин і близнят, утворення двійнят (при дотриманні зазначених вище умов) теж іноді потрібне[5].
- Діаграма Гассе підмножини відношень непорожнього перетину максимальних клік утворює орієнтоване дерево[6].
- Опуклі підмножини вершин (підмножини, що містять усі найкоротші шляхи між двома вершинами в підмножині) утворюють опуклу геометрію. Тобто будь-яку опуклу множину можна отримати з повного набору вершин послідовним видаленням крайніх вершин, тобто тих, що не належать якомусь найкоротшому шляху між рештою вершин[7]. У смарагді опуклу множину uxy не можна отримати таким способом, оскільки ні v, ні w не є крайніми.
Обчислювальна складність
Ґрунтуючись на описі орієнтованими деревами, птолемеєві графи можна розпізнати за лінійний час[6].
Примітки
- Kay, Chartrand, 1965, с. 342–346.
- Howorka, 1981, с. 323–331.
- Graphclass: ptolemaic. Information System on Graph Classes and their Inclusions. Процитовано 5 червня 2016..
- McKee, 2010, с. 651–661.
- Bandelt, Mulder, 1986, с. 182–208.
- Uehara, Uno, 2009, с. 1533–1543.
- Farber, Jamison, 1986, с. 433–444.
Література
- Hans-Jürgen Bandelt, Henry Martyn Mulder. . Distance-hereditary graphs // Journal of Combinatorial Theory. — 1986. — Т. 41, no. 2 (27 лютого). — С. 182–208. — (Series B). — DOI:.
- Martin Farber, Robert E. Jamison. . Convexity in graphs and hypergraphs // SIAM Journal on Algebraic and Discrete Methods. — 1986. — Т. 7, no. 3 (27 лютого). — С. 433–444. — DOI:.
- Edward Howorka. . A characterization of Ptolemaic graphs // Journal of Graph Theory. — 1981. — Т. 5, no. 3 (27 лютого). — С. 323–331. — DOI:.
- David C. Kay, Gary Chartrand. . A characterization of certain ptolemaic graphs // Canadian Journal of Mathematics. — 1965. — Т. 17 (27 лютого). — С. 342–346. — DOI:.
- Terry A. McKee. . Clique graph representations of Ptolemaic graphs // Discussiones Mathematicae Graph Theory. — 2010. — Т. 30, no. 4 (27 лютого). — С. 651–661. — DOI:.
- Ryuhei Uehara, Yushi Uno. . Laminar structure of Ptolemaic graphs with applications // Discrete Applied Mathematics. — 2009. — Т. 157, no. 7 (27 лютого). — С. 1533–1543. — DOI:.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.