Піфагорові середні
У математиці три класичні засоби Піфагорових середніх: середнє арифметичне (AM), середнє геометричне (GM) і середнє гармонійне (HM). Ці засоби були пропорційно вивчені піфагорійцями разом з пізнішим поколінням грецьких математиків[1], через їхню важливість у геометрії та музиці.
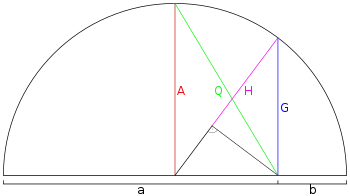

Визначення
Вони визначаються так:
Властивості
Кожне значення має наступні властивості:
- Збереження цінності
- Однорідна функція першої послідовності
- Інваріантність при обміні
- для будь-якої та .
- Виведення середньої величини
Гармонійні і арифметичні середні є взаємними двійниками один одного для позитивних аргументів:
в той час як середнє геометричне - це його власна взаємна подвійність:
Нерівності серед середніх
Існує впорядкування цих середніх (якщо всі позитивні)
з рівноправністю, тільки якщо всі рівні.
Це узагальнення нерівності арифметичних і геометричних середніх і окремий випадок нерівності для середнього степеневого. Доказ випливає з арифметико-геометричної середньої нерівності, та взаємної подвійності ( і також взаємні подвійні).
Вивчення піфагорових середніх тісно пов'язане з вивченням мажоризації й шур-опуклої функції. Гармонійними і геометричними середніми є увігнуті симетричні функції їхніх аргументів.
Примітки
- Heath, Thomas. History of Ancient Greek Mathematics.
Посилання
- Cantrell, David W. Pythagorean Means(англ.) на сайті Wolfram MathWorld. (на англ.)
- Nice comparison of Pythagorean means with emphasis on the harmonic mean (на англ.)
