Раціональний кубоїд

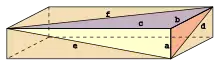
Раціональний кубоїд[1] (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед, у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами. Інакше кажучи, раціональний кубоїд — цілочисельний розв'язок системи діофантових рівнянь.

{\begin{cases}a^{2}+b^{2}=d^{2}\\a^{2}+c^{2}=e^{2}\\b^{2}+c^{2}=f^{2}\\a^{2}+b^{2}+c^{2}=g^{2}\end{cases}}

Раціональний кубоїд зі сторонами

a, b, c

стикаються з діагоналями

d, e, f

Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір показав, що якщо ідеальний кубоїд існує:

найменше ребро має бути більшим за 5 × 10¹¹.[2]
непарне ребро має бути більшим за 2.5 × 10¹³.[2]
просторова діагональ має бути більшою за 9 × 10¹⁵.[3]

Втім, знайдено безліч «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:

Edge кубоїд — кубоїд, у якого одне з ребер є нецілим числом. Найменший: із ребрами $(520, 576, \sqrt 618849)$ , лицьовими діагоналями $(776, 943, 975)$ , просторовою діагоналлю $1105$ ;
Face кубоїд — кубоїд, у якого одна з лицьових діагоналей є нецілим числом. Найменший: із ребрами $(104, 153, 672)$ , лицьовими діагоналями $(185, 680, \sqrt 474993)$ , просторовою діагоналлю $697$ ;
Body кубоїд (паралелепіпед Ейлера, див. нижче) — кубоїд, у якого просторова діагональ є нецілим числом. Найменший: із ребрами $(44, 117, 240)$ , лицьовими діагоналями $(125, 244, 267)$ , просторовою діагоналлю √73225;
Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута.

Також досі невідомо, чи існує раціональний прямокутний паралелепіпед у комплексних числах (Perfect Complex кубоїд). Втім, знайдено безліч «майже цілочисельних» паралелепіпедів у комплексних числах, у яких цілочисельними є всі величини, крім однієї:

Imaginary кубоїд — кубоїд, у якого одне з ребер є комплексним числом. Найменший: із ребрами $(\sqrt 3344 i, 60, 63)$ , лицьовими діагоналями $(16, 25, 87)$ , просторовою діагоналлю $65$ ;
Twilight кубоїд — кубоїд, у якого окрім ребра(ер), одна із лицьових діагоналей є комплексним числом. Найменший: із ребрами $(60i, \sqrt 3344, 65)$ , лицьовими діагоналями $(16i, 25, 87)$ , просторовою діагоналлю $63$ ;
Midnight кубоїд — кубоїд, у якого окрім ребра(ер), лицевої(их) діагоналі(ей), ще й просторова діагональ є комплексним числом. Найменший: із ребрами $(60i, 63i, \sqrt 3344 i)$ , лицьовими діагоналями $(16i, 25i, 87i)$ , просторова діагональ $65i$ ;

У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими.[4][5]

У вересні 2017 року проєкт розподілених обчислень yoyo@home (http://www.rechenkraft.net/yoyo/) розпочав підпроєкт Perfect Cuboid, що займається пошуком кубоїдів у натуральних числах: Perfect, Edge, Face (повністю), а також деяких видів кубоїдів у комплексних числах (Perfect Complex, Imaginary та Twilight). Станом на жовтень 2018 року підпроєкт стверджує, що якщо ідеальний кубоїд існує, його просторова діагональ має бути більша за 2⁵³ ≈ 9 × 10¹⁵.[3]

Паралелепіпед Ейлера

Прямокутний паралелепіпед, у якого цілочисельні ребра і лицьові діагоналі, називається ейлеровим. Найменший з паралелепіпедів Ейлера — з ребрами (44, 117, 240) та лицьовими діагоналями (125, 244, 267).

Деякі інші маленькі паралелепіпеди Ейлера в форматі: ребра $(a, b, c)$ — лицьові діагоналі $(d, e, f)$ :

(	85,	132,	720	) — (	157,	725,	732	)
(	140,	480,	693	) — (	500,	707,	843	)
(	160,	231,	792	) — (	281,	808,	825	)
(	187,	1020,	1584	) — (	1037,	1595,	1884	)
(	195,	748,	6336	) — (	773,	6339,	6380	)
(	240,	252,	275	) — (	348,	365,	373	)
(	429,	880,	2340	) — (	979,	2379,	2500	)
(	495,	4888,	8160	) — (	4913,	8175,	9512	)
(	528,	5796,	6325	) — (	5820,	6347,	8579	)

Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає.

Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини) [6]:

Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1).
Одне ребро ділиться на 3 і ще одне — на 9.
Одне ребро ділиться на 5.
Одне ребро ділиться на 11.
Одне ребро ділиться на 19.
Одне ребро або просторова діагональ діляться на 13.
Одне ребро, лицьова або просторова діагональ діляться на 17.
Одне ребро, лицьова або просторова діагональ діляться на 29.
Одне ребро, лицьова або просторова діагональ діляться на 37.

Додатково:

Просторова діагональ примітивного ідеального кубоїда має бути добутком виключно простих n виду $n \equiv 1 (mod 4)$

Прямокутний паралелепіпед у комплексних числах

Відомі такі властивості прямокутних паралелепіпедів у комплексних числах:

Існування будь-якого Face кубоїда тягне за собою існування 2-х різних Imaginary кубоїдів. Наприклад:

Face кубоїд із ребрами $(104, 153, 672)$ , лицьовими діагоналями $(185, 680, \sqrt 474993)$ , просторова діагональ $697$ тягне за собою:

Imaginary кубоїд із ребрами $(104i, 185, 680)$ , лицьовими діагоналями $(153, 672, \sqrt 496625)$ , просторовою діагоналлю $697$ ;
Imaginary кубоїд із ребрами $(153i, 185, 672)$ , лицьовими діагоналями $(104, \sqrt 428175, 697)$ , просторовою діагоналлю $680$ .

Існування будь-якого Edge, Face, Body або Imaginary кубоїда тягне за собою існування 3-х різних Twilight кубоїда. Наприклад:

Face кубоїд із ребрами $(104, 153, 672)$ , лицьовими діагоналями $(185, 680, \sqrt 474993)$ , просторовою діагоналлю $697$ тягне за собою:

Twilight кубоїд із ребрами $(153i, 104i, 697)$ , лицьовими діагоналями $(185i, 680, \sqrt 474993)$ , просторовою діагоналлю $672$ ;
Twilight кубоїд із ребрами $(672і, 104і, 697)$ , лицьовими діагоналями $(680i, 185, \sqrt 474993)$ , просторовою діагоналлю $153$ ;
Twilight кубоїд із ребрами $(672і, 153і, 697)$ , лицьовими діагоналями $(\sqrt 474993 i, 153, 672)$ , просторовою діагоналлю $104$ .

Існування будь-якого Edge, Face, Body, Imaginary або Twilight кубоїда тягне за собою існування Midnight кубоїда, що утворюється шляхом добутку усіх його величин на уявну одиницю $i$ .

Існування будь-якого Раціонального кубоїда у натуральних числах тягне за собою існування ще 7 різних Раціональних кубоїдів у комплексних числах (3 Perfect Complex та 4 Perfect Midnight кубоїдів):

Припустимо, що існує Ідеальний кубоїд із ребрами $(A, B, С)$ , лицьовими діагоналями $(D, E, F)$ та просторовою діагоналлю $G$ , тоді мають місце також:

Perfect Complex із ребрами $(Bi, Ci, G)$ , лицьовими діагоналями $(Fi, E, D)$ та просторовою діагоналлю $A$ ;
Perfect Complex із ребрами $(Ai, Ci, G)$ , лицьовими діагоналями $(Ei, F, D)$ та просторовою діагоналлю $B$ ;
Perfect Complex із ребрами $(Bi, Ai, G)$ , лицьовими діагоналями $(Di, E, F)$ та просторовою діагоналлю $C$ ;
Perfect Midnight із ребрами $(Ai, Bi, Ci)$ , лицьовими діагоналями $(Di, Ei, Fi)$ та просторовою діагоналлю $Gi$ ;
Perfect Midnight із ребрами $(B, C, Gi)$ , лицьовими діагоналями $(F, Ei, Di)$ та просторовою діагоналлю $Ai$ ;
Perfect Midnight із ребрами $(A, C, Gi)$ , лицьовими діагоналями $(E, Fi, Di)$ та просторовою діагоналлю $Bi$ ;
Perfect Midnight із ребрами $(B, A, Gi)$ , лицьовими діагоналями $(D, Ei, Fi)$ та просторовою діагоналлю $Ci$ ;

Див. також

Відкриті математичні проблеми

Примітки

Perfect Cuboid на сайті Wolfram MathWorld
R Matson, Results of a Computer Search for a Perfect Cuboid, http://unsolvedproblems.org/S58.pdf
Yoyo@Home, Perfect Cuboid sub-project, http://www.rechenkraft.net/yoyo/
Lasha Margishvili "The Diophantine Rectangular Parallelepiped (A Perfect Cuboid)": part 1, part 2
Mu Alpha Theta. Архів оригіналу за 26 листопада 2006. Процитовано 26 листопада 2006.
Primitive Euler Bricks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Perfect Cuboid на сайті Wolfram MathWorld

[Matson-2] R Matson, Results of a Computer Search for a Perfect Cuboid, http://unsolvedproblems.org/S58.pdf

[yoyo@home-3] Yoyo@Home, Perfect Cuboid sub-project, http://www.rechenkraft.net/yoyo/

[4] Lasha Margishvili "The Diophantine Rectangular Parallelepiped (A Perfect Cuboid)": part 1, part 2

[5] Mu Alpha Theta. Архів оригіналу за 26 листопада 2006. Процитовано 26 листопада 2006.

[f2-6] Primitive Euler Bricks