Рекурсивна нейронна мережа

Рекурси́вні нейро́нні мере́жі (РНМ, англ. recursive neural networks, RNN) — це клас глибинних нейронних мереж, створюваних рекурсивним застосуванням одного й того ж набору ваг до структури, щоби здійснювати Структурове передбачування вхідних структур мінливого розміру, або скалярне передбачування на них, шляхом обходу заданої структури в топологічній послідовності. РНМ були успішними, наприклад, в навчанні послідовнісних та деревних структур в обробці природної мови, головним чином неперервних представлень фраз та речень на основі векторного представлення слів. Вперше РНМ було введено для навчання розподілених представлень структури, таких як терміни логіки.[1] Моделі та загальні схеми було розроблено в подальших працях, починаючи з 1990-х років.[2][3]

Архітектури

Базова
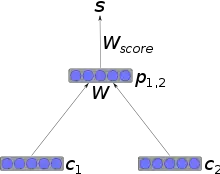
Архітектура простої рекурсивної мережі

У випадку найпростішої архітектури вузли поєднуються у батьківські із застосуванням вагової матриці, яка є спільною для всієї мережі, та нелінійності, такої як гіперболічний тангенс. Якщо c1 та c2 є n-мірними векторними представленнями вузлів, то їхній батьківський вузол також буде n-мірним вектором, що обчислюється як

де W є навченою ваговою матрицею .

Цю архітектуру, з деякими поліпшеннями, було застосовано для успішного розбору природних сцен та для синтаксичного розбору речень природної мови.[4]

Рекурсивна каскадна кореляція

Рекурсивна каскадна кореляція (РекКК, англ. Recursive Cascade Correlation, RecCC) є конструктивним нейромережевим підходом до деревних областей[2] з новаторськими застосуваннями в хімії[5] та розширенням для орієнтованих ациклічних графів.[6]

Некерована РНМ

Систему для некерованих РНМ (англ. Unsupervised RNN) було представлено в працях [7][8].

Тензорна

Рекурсивні нейронні тензорні мережі (англ. recursive neural tensor networks) використовують одну функцію поєднання на основі тензорів для всіх вузлів дерева.[9]

Тренування

Стохастичний градієнтний спуск

Як правило, для тренування таких мереж застосовують стохастичний градієнтний спуск (СГС, англ. stochastic gradient descent, SGD). Градієнт обчислюють, застосовуючи зворотне поширення структурою (ЗПС), що є варіацією зворотного поширення в часі, яке використовують для рекурентних нейронних мереж.

Властивості

В літературі було доведено здатність РНМ до універсального наближення над деревами.[10][11]

Пов'язані моделі

Рекурентні нейронні мережі

Рекурентні нейронні мережі є рекурсивними штучними нейронними мережами з певною структурою: такою, як в лінійного ланцюжка. В той час як рекурсивні нейронні мережі працюють на будь-якій ієрархічній структурі, поєднуючи дочірні представлення в батьківські, рекурентні нейронні мережі діють на лінійній послідовності часу, поєднуючи попередній такт і приховане представлення в представлення поточного такту.

Деревні мережі з відлунням стану

Дієвий підхід до втілення РНМ дають деревні мережі з відлунням стану (англ. Tree Echo State Networks)[12] в рамках парадигми резервуарного обчислення.

Розширення для графів

До розширень для графів належать графова нейронна мережа (ГНМ, англ. Graph Neural Network, GNN),[13] нейронна мережа для графів (НМДГ, англ. Neural Network for Graphs, NN4G)[14] та новіші згорткові нейронні мережі для графів.

Примітки
  1. Goller, C.; Küchler, A. Learning task-dependent distributed representations by backpropagation through structure. Neural Networks, 1996., IEEE. doi:10.1109/ICNN.1996.548916. (англ.)
  2. Sperduti, A.; Starita, A. (1 травня 1997). Supervised neural networks for the classification of structures. IEEE Transactions on Neural Networks 8 (3): 714–735. ISSN 1045-9227. doi:10.1109/72.572108. (англ.)
  3. Frasconi, P.; Gori, M.; Sperduti, A. (1 вересня 1998). A general framework for adaptive processing of data structures. IEEE Transactions on Neural Networks 9 (5): 768–786. ISSN 1045-9227. doi:10.1109/72.712151. (англ.)
  4. Socher, Richard; Lin, Cliff; Ng, Andrew Y.; Manning, Christopher D. Parsing Natural Scenes and Natural Language with Recursive Neural Networks. The 28th International Conference on Machine Learning (ICML 2011). (англ.)
  5. Bianucci, Anna Maria; Micheli, Alessio; Sperduti, Alessandro; Starita, Antonina (2000). Application of Cascade Correlation Networks for Structures to Chemistry. Applied Intelligence (англ.) 12 (1-2): 117–147. ISSN 0924-669X. doi:10.1023/A:1008368105614. (англ.)
  6. Micheli, A.; Sona, D.; Sperduti, A. (1 листопада 2004). Contextual processing of structured data by recursive cascade correlation. IEEE Transactions on Neural Networks 15 (6): 1396–1410. ISSN 1045-9227. doi:10.1109/TNN.2004.837783. (англ.)
  7. Hammer, Barbara; Micheli, Alessio; Sperduti, Alessandro; Strickert, Marc (2004). Recursive self-organizing network models. Neural Networks 17: 1061–1085. (англ.)
  8. Hammer, Barbara; Micheli, Alessio; Sperduti, Alessandro; Strickert, Marc (1 березня 2004). A general framework for unsupervised processing of structured data. Neurocomputing 57: 3–35. doi:10.1016/j.neucom.2004.01.008. (англ.)
  9. Socher, Richard; Perelygin, Alex; Y. Wu, Jean; Chuang, Jason; D. Manning, Christopher; Y. Ng, Andrew; Potts, Christopher. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank. EMNLP 2013. (англ.)
  10. Hammer, Barbara (3 жовтня 2007). Learning with Recurrent Neural Networks (англ.). Springer. ISBN 9781846285677. (англ.)
  11. Hammer, Barbara; Micheli, Alessio; Sperduti, Alessandro (1 травня 2005). Universal Approximation Capability of Cascade Correlation for Structures. Neural Computation (англ.) 17 (5): 1109–1159. doi:10.1162/0899766053491878. (англ.)
  12. Gallicchio, Claudio; Micheli, Alessio (4 лютого 2013). Tree Echo State Networks. Neurocomputing 101: 319–337. doi:10.1016/j.neucom.2012.08.017. (англ.)
  13. Scarselli, F.; Gori, M.; Tsoi, A. C.; Hagenbuchner, M.; Monfardini, G. (1 січня 2009). The Graph Neural Network Model. IEEE Transactions on Neural Networks 20 (1): 61–80. ISSN 1045-9227. doi:10.1109/TNN.2008.2005605. (англ.)
  14. Micheli, A. (1 березня 2009). Neural Network for Graphs: A Contextual Constructive Approach. IEEE Transactions on Neural Networks 20 (3): 498–511. ISSN 1045-9227. doi:10.1109/TNN.2008.2010350. (англ.)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.