Деформація згину
Деформа́ція зги́ну або згин — тип деформації бруса (балки), що полягає у викривленні осі прямого бруса чи зміні кривини осі кривого бруса в результаті виникнення згинальних моментів у його перерізах від прикладених навантажень (поперечних сил і/або згинальних моментів у площині, що проходить через вісь бруса).

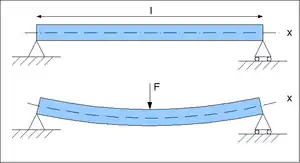
Локальна деформація різних частин тіла при згинанні різна. Наприклад, у випадку, зображеному на рисунку, верхня частина балки стискається, а нижня — розтягується.
Основні поняття
Переміщення будь-якої точки осі балки, котра працює на згин, виражається вектором, початок якого суміщено з початковим положенням точки, а кінець — з положенням цієї самої точки у деформованій балці. У прямих балках переміщення точок які спрямовані перпендикулярно до початкового положення осі, називають прогинами і позначається . При згинанні відбувається також поворот перерізів стержня навколо осей, що лежать у площинах перерізів і позначається .
Умовна назва кривої лінії, що її форми набуває вісь балки (бруса) при згині у межах пружної деформації носить назву пружна лінія.
Види згину
Стосовно до бруса розрізняють згин плоский, або простий, та складний. При плоскому (простому) згині зовнішні сили діють в одній з головних площин бруса (вони проходять через вісь бруса і головні осі інерції поперечного перерізу, див. Моменти інерції плоских перерізів), при складному згині — в різних площинах. Різновидом складного є косий згин, коли навантаження діють у площині, що не збігається з будь-якою з головних площин.
Залежно від сил, що діють у поперечному перерізі бруса, згин буває чистим (при наявності лише згинальних моментів), поперечним (діють поперечні сили), поздовжнім (випинання під впливом стискувальних сил, спрямованих вздовж осі) і поперечно-поздовжнім.
Розрахунки при згині
Класична теорія
Наближений розрахунок прямого бруса на дію згину у пружній стадії на основі класичної теорії (теорії Ейлера-Бернуллі) проводиться виходячи з наступних допущень:
- поперечні перерізи, що були плоскими і перпендикулярними до осі балки до деформації, залишаються плоскими і перпендикулярними до її зігнутої осі (пружної лінії) після деформування (гіпотеза плоских перерізів);
- поздовжні волокна бруса при згині не тиснуть одне на одного і не намагаються відірватись одне від одного;
- переміщення і деформації вважаються малими а балка — нерозтяжною;
- розміри перерізів балки вважаються малими у порівняння з радіусом кривини осі балки;
- матеріал балки розглядається як лінійно пружний, що описується законом Гука
При плоскому згині в будь-якій точці поперечного перерізу балки виникають нормальні (σ) і дотичні (τ) напруження. Нормальні напруження визначають за формулою Нав’є:
де: Mz — згинальний момент;
- y — координата досліджуваної точки відносно нейтральної лінії;
- Iz — момент інерції відносно нейтральної лінії.
Дотичні напруження визначають за формулою Д. І. Журавського:
де Qy — поперечна сила у перерізі;
- Sz — статичний момент відносно нейтральної осі частини площі поперечного перерізу, що розташована вище (або нижче) волокна, що розглядається;
- b — ширина перерізу на рівні волокна, що розглядається.
Характер зміни згинальних моментів і поперечних сил по довжині бруса зазвичай зображується графіками (епюрами), за якими визначаються їх розрахункові значення.
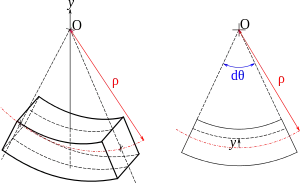
Ступінь викривлення осі у межах пружності залежить від величини згинального моменту і жорсткості бруса. Кривина осі визначається виразом:
де ρ — радіус кривини осі зігнутого бруса у розглянутому перерізі; Е — модуль Юнга матеріалу бруса а Iz — момент інерції. Добуток EIz називають жорсткістю балки на згин[1];
Для випадку малих деформацій кривина наближено виражається другою похідною від прогину , а тому між координатами зігнутої осі та згинальним моментом існує диференціальна залежність:
що називається диференціальним рівнянням осі зігнутого бруса. Його рішення називається рівнянням пружної лінії балки (бруса).
Відносна деформація при згині визначається як: ε, ε, де h - висота балки.
У практичних дослідах на згин для визначення відносної деформації ε вимірюють прогини зразків. Взаємозв’язок між прогином f , що вимірюється між внутрішніми роликами, розташованими на відстані l0, за чотириточковим (круговим) згином та радіусом кривизни ρ наступний:
. Тоді ε. Для триточкового згину ця формула буде натупною: ε.
Теорія балок Тимошенка
Дана теорія базується на тих же гіпотезах, що й класична, однак гіпотеза плоских перерізів має модифікований вид: приймається, що перерізи, які були до деформації плоскими і нормальними до осі балки, залишаються плоскими, але перестають бути нормальними до зігнутої осі. Таким чином, дана теорія враховує деформацію зсуву й дотичні напруження. Врахування дотичних напружень є важливим для композитів та матеріалів, що мають шарувату структуру (деревина), оскільки руйнування може відбуватись по лінії розмежування шарів від зсуву.
Основні залежності:
де — модуль зсуву матеріалу балки, — площа перерізу, — коефіцієнт, що враховує нерівномірність розподілу дотичних напружень по перерізу і залежить від його форми. Величина
є кутом зсуву.
Див. також
Посилання
- Згин // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 99. — ISBN 978-966-7407-83-4.
- Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993. — 655 с. ISBN 5-11-004083-4
- Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб'юк В. І. — К., 2009. — 380 с.
- Мильніков О. В. Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. — Т.: Видавництво ТНТУ, 2010. — 257 с.
| Види деформацій | |
| Розтяг-стиск | Зсув | Кручення | Згин | |