Сигмоїда
Сигмоїда — це неперервно диференційована монотонна нелінійна S-подібна функція, яка часто застосовується для «згладжування» значень деякої величини.
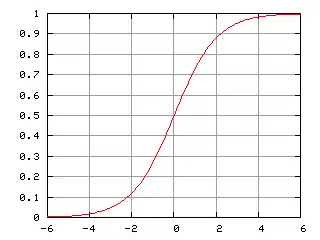
Часто під сигмоїдою розуміють логістичну криву (див. рисунок ліворуч), яка визначається формулою
Родина функцій класу сигмоїд
У родину функцій класу сигмоїд також входять такі функції як арктангенс, гіперболічний тангенс та інші.
Функція Фермі (Експоненційна сигмоїда):
Раціональна сигмоїда:
Гіперболічний тангенс:
Застосування
Сигмоїда застосовується в нейронних мережах[1] для того, щоб ввести деяку нелінійність в роботу мережі, але при цьому не дуже сильно змінити результат її роботи.
Одна з причин через яку сигмоїда використовується в нейронних мережах — це простий вираз її похідної через саму функцію (що дозволило істотно скоротити обчислювальну складність методу зворотного поширення помилки, зробивши його придатним на практиці):
Не менш важливою причиною введення нелінійності є математично доведена можливість отримати як завгодно точне наближення будь-якої неперервної функції багатьох змінних, використовуючи операції додавання та множення на число, суперпозицію функцій, лінійні функції, а також одну довільну неперервну нелінійну функцію однієї змінної.[2][3]
Див. також
Посилання
- Порівняння швидкості кількох програмних реалізацій гіперболічного тангенсу
- Узагальнена апроксимаційний теорема та обчислювальні можливості нейронних мереж. Архів оригіналу за 4 квітня 2010. Процитовано 25 січня 2010.
- О произвольной нелинейности нейрона в нейросети
