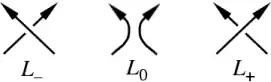Скейн-співвідношення
Центральне питання теорії вузлів — чи відображають дві діаграми один і той самий вузол. Один з інструментів, що використовуються для відповіді на це питання — многочлен вузла, який є інваріантом вузла. Якщо двом діаграмам відповідають різні многочлени, то вони подають різні вузли. Обернене не завжди істинне.
Скейн-співвідношення (або співвідношення типу Конвея) часто використовують, щоб простим способом визначити многочлен вузла. Неформально кажучи, скейн-співвідношення задає лінійний зв'язок значень многочлена вузла на трьох зачепленнях, які відрізняються одне від одного лише в малій ділянці. Для деяких многочленів, таких як многочлени Конвея, Александера і Джонса, відповідного скейн-співвідношення достатньо, щоб обчислити многочлен рекурсивно. Для інших, таких як многочлен HOMFLY, потрібні складніші алгоритми.
Визначення
У скейн-співвідношенні беруть участь три діаграми зачеплення, ідентичні всюди, крім одного перехрестя. Ці три діаграми мають виражати три можливості, які могли б мати місце на цьому перехресті: нитка може пройти під іншою ниткою, над нею або НЕ перетнутися з нею зовсім. Необхідно розглядати діаграми зачеплень, оскільки зміна навіть одного перехрестя може перетворити діаграму вузла на діаграму зачеплення і навпаки. Залежно від конкретного многочлена вузла, зачеплення, що з'являються в скейн-співвідношенні можуть бути орієнтованими або неорієнтованими.
Три діаграми позначаються так. Розгорніть вузол так, щоб напрямки обох ниток у розглянутому перетині вказували приблизно на північ. В однієї діаграми нитка північно-західного напрямку проходить над північно-східною ниткою, її позначимо . В іншої діаграми північно-східна нитка проходить над північно-західною, це . Остання діаграма не має цього перетину і позначається .
(Насправді, позначення не залежить від напрямку в тому сенсі, що після заміни всіх напрямків на протилежні, позначення залишається колишнім. Тому многочлени визначаються однозначно і на неорієнтованих вузлах. Однак орієнтація на зачепленні принципово важлива, щоб пам'ятати, в якому порядку виконувалася рекурсія.)
Корисно уявляти це як складання з однієї діаграми двох інших накладенням «латок» з відповідними орієнтаціями.
Щоб рекурсивно визначити многочлен вузла (зачеплення), фіксується функція і для будь-якої трійки діаграм і їхніх многочленів, позначених, як було зазначено вище,
або акуратніше
- для кожного .
(Знаходження функції , яка робить многочлен незалежним від черговості перетинів у рекурсії — непроста задача.)
Формальніше, скейн-співвідношення можна розглядати, як визначення ядра фактор-відображення з планарної алгебри сплетінь. Таке відображення відповідає многочлену вузла, якщо всі замкнуті діаграми відображати в складні види порожніх діаграм.