Сферична теорема Піфагора
Сфери́чна теоре́ма Піфаго́ра — теорема, що встановлює співвідношення між сторонами прямокутного сферичного трикутника.
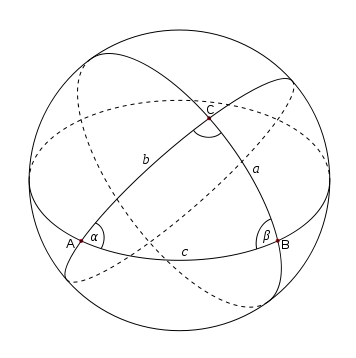
Формулювання і доведення
Сферична теорема Піфагора формулюється так[1]:
| Косинус гіпотенузи прямокутного сферичного трикутника дорівнює добутку косинусів його катетів. |
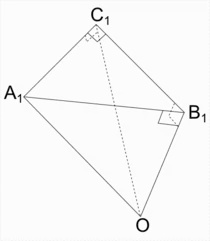
Доказ проведемо за допомогою тригранного кута[1] OA1B1C1 зі сторонами (променями) OA1, OB1, OC1 і вершиною в точці O, плоскі кути A1OC1 і C1OB1 якого дорівнюють катетам b і a даного трикутника, плоский кут A1OB1 дорівнює його гіпотенузі c, двогранний кут між гранями A1OC1 і C1OB1 дорівнює 90 градусів, а інші два двогранних кути дорівнюють відповідним кутам прямокутного сферичного трикутника. Цей тригранний кут перетинає площина A1B1C1, перпендикулярна до променя OB1. Тоді кути A1C1O і A1C1B1 будуть прямими.
Зауважимо, що
Звідси
Що й потрібно було довести.
Якщо вважати, що сферичну теорему косинусів уже доведено, формулу для сферичної теореми Піфагора можна зразу отримати з неї, записавши сферичну теорему косинусів для гіпотенузи даного прямокутного сферичного трикутника і просто підставивши в отриманий вираз кут 90°, косинус якого дорівнює нулю.
Наслідки і застосування
За радіусу сфери, що прямує до нескінченності, сферична теорема Піфагора переходить у теорему Піфагора планіметрії. Тому, оскільки радіус Землі великий, за невеликих відстаней прямокутні трикутники на поверхні Землі (наприклад, використовувані для вимірювання відстаней і кутів на місцевості) практично підпорядковуються теоремі Піфагора планіметрії[2], тоді як для великих відстаней, порівнянних з радіусом Землі, вже необхідно застосовувати сферичну теорему Піфагора.
Застосувавши сферичну теорему Піфагора, можна отримати формули для різниці довгот і відстані між точками земної поверхні, а, отже, й відповідні формули для відстаней і координат точок на небесній сфері.
Зі сферичної теореми Піфагора випливає, що в прямокутному сферичному трикутнику кількість сторін, менших від 90°, непарна, а більших — парна[1]. Тому якщо обидва катети прямокутного сферичного трикутника більші від 90°, то його гіпотенуза менша від 90°, тобто в цьому випадку гіпотенуза коротша від кожного з двох катетів — положення, неможливе для прямокутного трикутника на площині.
Історія
Сферична теорема Піфагора була відома ще Аль-Біруні, який разом з тим не знав сферичної теореми косинусів, тому застосував сферичну теорему Піфагора і теорему синусів для розв'язання принаймні двох задач: визначення різниці довгот двох пунктів на поверхні Землі за їх широтами і відстанню між ними і визначення відстані між двома пунктами на поверхні Землі за їх широтами і довготами[3].
Див. також
Примітки
- Степанов Н.Н. Сферическая теорема Пифагора // Сферическая тригонометрия. — М.—Л. : ОГИЗ, 1948. — С. 42—44.
- John McCleary. Geometry from a differentiable viewpoint. — Cambridge University Press, 1994. — С. 6.
- Розенфельд Б.А., Рожанская М.М. Астрономический труд Ал-Бируни «Канон Мас'уда» // Историко-астрономические исследования. — М. : Наука, 1969. — Вип. X (28 січня). — С. 63—96.