Теорема косинусів (сферична геометрія)

В сферичній тригонометрії, теорема косинусів (також відома як правило косинусів для сторін[1]) — формули відношення сторін і кутів сферичних трикутників, аналог теореми косинусів в тригонометрії на площині.

Сферичний трикутник

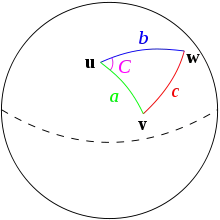
Нехай дана сфера з діаметром 1, сферичний трикутник на сфері визначається трьома великими колами, що поєднують три точки u , v і w на сфері (див. малюнок праворуч). Якщо довжини трьох сторін становлять a (від u' до v), b (від u до w) і c (від v до w), і кут навпроти c є C, тоді (перший) сферична теорема косинусів стверджує:[2][1]

\cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C).\,

Через те, що це одинична сфера, довжини a, b і c просто дорівнюють кутам (в радіанах) утвореним радіусами сфери проведеними до кінців відповідної сторони (для не одиничної сфери довжини сторін дорівнюють добутку дугового кута на радіус). В особливому випадку, коли $C=\pi /2$ , тоді $\cos(C)=0\,$ і ми отримуємо сферичний аналог теореми Піфагора:

\cos(c)=\cos(a)\cos(b).\,

Різновидом теореми косинусів, друга сферична теорема косинусів,[3] (також відома як правило косинусів для кутів[1]) стверджує:

\cos(A)=-\cos(B)\cos(C)+\sin(B)\sin(C)\cos(a)\,

де A та B це кути протилежні до сторін a і b, відповідно.

Для маленького сферичного трикутника, тобто для маленьких a, b і c, сферична теорема косинусів наближається до теореми косинусів на площині,

c^{2}\approx a^{2}+b^{2}-2ab\cos(C).\,\!

Помилка в цьому наближенні, може бути обчислена з ряду Тейлора для функцій косинуса та синуса, і становить:

O(c^{4})+O(a^{3}b)+O(ab^{3}).\,\!

Доведення

Доведення може бути побудоване наступним чином.[2] Нехай u, v, і w означають одиничні вектори з центру сфери до кутів трикутника. Тоді, довжини (кути) сторін задаються як скалярні добутки:

\cos(a)=\mathbf {u} \cdot \mathbf {v}

\cos(b)=\mathbf {u} \cdot \mathbf {w}

\cos(c)=\mathbf {v} \cdot \mathbf {w}

Для отримання кута C, нам потрібен дотичні вектори t_a і t_b в u уздовж напрямків сторін a і b, відповідно. Наприклад, дотичний вектор t_a це одиничний вектор перпендикулярний до u в площині u-v, напрямок якого задається компонентом v перпендикулярним до u. Це означає:

\mathbf {t} _{a}={\frac {\mathbf {v} -\mathbf {u} (\mathbf {u} \cdot \mathbf {v} )}{\left|\mathbf {v} -\mathbf {u} (\mathbf {u} \cdot \mathbf {v} )\right|}}={\frac {\mathbf {v} -\mathbf {u} \cos(a)}{\sin(a)}}

.

Аналогічно,

\mathbf {t} _{b}={\frac {\mathbf {w} -\mathbf {u} \cos(b)}{\sin(b)}}.

Тоді кут C отримаємо як:

\cos(C)=\mathbf {t} _{a}\cdot \mathbf {t} _{b}={\frac {\cos(c)-\cos(a)\cos(b)}{\sin(a)\sin(b)}}

звідки негайно отримуємо теорему косинусів.

Як наслідок легко отримати другу теорему косинусів.

Теорема синусів для тригранного кута

${\sin a \over \sin A}={\sin b \over \sin B}={\sin c \over \sin C}$ .

Примітки

W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).
Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).
Reiman, István (1999). Geometria és határterületei. Szalay Könyvkiadó és Kereskedőház Kft. с. 83.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[VNR-1] W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).

[Ireneus-2] Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).

[3] Reiman, István (1999). Geometria és határterületei. Szalay Könyvkiadó és Kereskedőház Kft. с. 83.