Теорема про чотири вершини
Теорема про чотири вершини стверджує, що функція кривини простої замкнутої гладкої плоскої кривої має щонайменше чотири локальних екстремуми (зокрема, щонайменше два локальних максимуми і щонайменше два локальних мінімуми). Назва теореми відображає угоду називати екстремальні точки функції кривини вершинами. Ця теорема має багато узагальнень, включно з версією кривої у просторі, де вершина визначається як точка в якій зникає скрут кривої.
Приклади
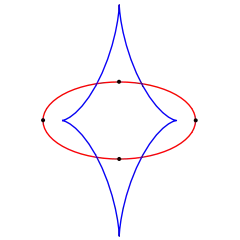
Еліпс має в точності чотири вершини — два локальних максимуми кривини в місцях перетину еліпса з великою віссю, і два локальних мінімуми в місцях перетину з малою віссю. На колі всі точки є як локальними максимумами, так і локальними мінімумами кривини, так що на ній нескінченно багато вершин.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.