Скрут кривої

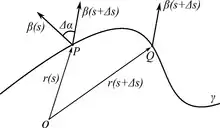
Нехай ${\displaystyle P}$ — довільна точка регулярної кривої ${\displaystyle \gamma }$, ${\displaystyle Q}$ — точка кривої, що близька до ${\displaystyle P}$. Позначимо через ${\displaystyle \Delta \alpha }$ кут між стичними площинами кривої в точках ${\displaystyle P}$ та ${\displaystyle Q}$, а через ${\displaystyle \Delta s}$ — довжину дуги ${\displaystyle PQ}$ кривої. Тоді ${\displaystyle \lim _{Q\to P}{\frac {\Delta \alpha }{\Delta s}}}$, якщо він існує, називається абсолютним скрутом кривої ${\displaystyle \gamma }$ в точці ${\displaystyle P}$ і позначається через ${\displaystyle |k_{2}|}$[1].

Абсолютний скрут кривої в точці ${\displaystyle P}$ дорівнює кутовій швидкості обертання бінормалі кривої навколо точки ${\displaystyle Q}$, тобто ${\displaystyle |k_{2}|=\lim _{\Delta s\to 0}{\frac {\Delta \alpha }{\Delta s}},}$ де ${\displaystyle \Delta \alpha }$ — кут повороту бінормалі, що відповідає приросту довжини дуги ${\displaystyle \Delta s}$. Скрут буде додатнім (від'ємним), якщо при спостереженні з кінця вектора швидкості вектор бінормалі при русі точки по кривій обертається проти (по) годинникової стрілки.

${\displaystyle |k_{2}|=|{\bar {\beta }}'_{s}|={\frac {|({\bar {r}}'_{s},{\bar {r}}''_{s},{\bar {r}}'''_{s})|}{k_{1}^{2}}}}$, 

Доведення. Розглянемо властивості вектора ${\displaystyle {\bar {\beta }}}$:

1. ${\displaystyle {\bar {\beta }}'\bot {\bar {\beta }}}$, бо ${\displaystyle {\bar {\beta }}}$ — одиничний вектор, отже ${\displaystyle {\bar {\beta }}^{2}=const}$, ${\displaystyle 2{\bar {\beta }}{\bar {\beta }}'=0}$;
2. ${\displaystyle {\bar {\beta }}'\bot {\bar {\tau }}}$ (оскільки ${\displaystyle {\bar {\beta }}=[{\bar {\tau }},{\bar {\nu }}]}$, з першої формули Френе: ${\displaystyle {\frac {d{\bar {\tau }}}{ds}}=k_{1}{\bar {\nu }}}$ і ${\displaystyle {\frac {d{\bar {\beta }}}{ds}}=[{\frac {d{\bar {\tau }}}{ds}},{\bar {\nu }}]+[{\bar {\tau }},{\frac {d{\bar {\nu }}}{ds}}]=[{\bar {\tau }},{\bar {\nu }}']}$); Тут ${\displaystyle {\bar {\tau }},{\bar {\nu }}}$ познадають відповідно одиничні дотичний і нормальний вектори, ${\displaystyle k_{1}}$— кривину кривої у відповідній точці.
3. ${\displaystyle {\frac {d{\bar {\beta }}}{ds}}=-k_{2}{\bar {\nu }}}$ (третя формула Френе).

Таким чином, ${\displaystyle |k_{2}|={\frac {|{d{\bar {\beta }}}|}{|ds|}}}$.

Знайдемо тепер ${\displaystyle {\frac {|{d{\bar {\beta }}}|}{|ds|}}}$, ${\displaystyle {\bar {\beta }}'=-k_{2}{\bar {\nu }}}$, ${\displaystyle {\bar {\beta }}'\cdot {\bar {\nu }}=-k_{2}{\bar {\nu }}^{2}}$ або ${\displaystyle k_{2}={\bar {\beta }}'\cdot {\nu }^{2}}$.

Враховуючи властивість 2 та першу формулу Френе і розглядаючи кривину ${\displaystyle k}$ як функцію ${\displaystyle s}$, маємо:

${\displaystyle k_{2}=[{\bar {\tau }},{\bar {\nu }}']\cdot {\bar {\nu }}=-[{\bar {r}}',({\frac {1}{k_{1}}}{\bar {r}}'')']\cdot {\frac {1}{k_{1}}}{\bar {r}}''=-{\frac {1}{k_{1}^{3}}}[{\bar {r}}',{\bar {r}}'''k_{1}-{\bar {r}}''k_{1}']{\bar {r}}''={\frac {1}{k_{1}^{3}}}([{\bar {r}}',{\bar {r}}'']k_{1}'{\bar {r}}''-[{\bar {r}}',{\bar {r}}''']{\bar {r}}''k_{1})={\frac {({\bar {r}}',{\bar {r}}'',{\bar {r}}''')}{k_{1}^{2}}}}$.

Отже, ${\displaystyle |k_{2}|={\frac {|({\bar {r}}'_{s},{\bar {r}}''_{s},{\bar {r}}'''_{s})|}{k_{1}^{2}}}}$

Обчислимо скрут гвинтової лінії: ${\displaystyle {\begin{cases}x(t)=a\cdot \cos t,\\y(t)=a\cdot \sin t,\\z(t)=b\cdot t,\end{cases}}}$. Оскільки

${\displaystyle {\bar {r}}'_{t}=(-a\cdot \sin t,a\cdot \cos t,b);}$

${\displaystyle {\bar {r}}''_{t}=(-a\cdot \cos t,-a\cdot \sin t,0);}$

${\displaystyle {\bar {r}}'''_{t}=(a\cdot \sin t,-a\cdot \cos t,0),}$

то

${\displaystyle <{\bar {r}}',{\bar {r}}'>=a^{2}+b^{2},}$

${\displaystyle <{\bar {r}}'',{\bar {r}}''>=a^{2},}$

${\displaystyle <{\bar {r}}',{\bar {r}}''>=0;}$

${\displaystyle [{\bar {r}}',{\bar {r}}'']^{2}={\bar {r}}'^{2}{\bar {r}}''^{2}-<{\bar {r}}',{\bar {r}}''>^{2}=(a^{2}+b^{2})a^{2};}$

${\displaystyle ({\bar {r}}',{\bar {r}}'',{\bar {r}}''')=ba^{2}.}$

Тоді

${\displaystyle k_{2}=-{\frac {b}{a^{2}+b^{2}}}.}$

• Борисенко, О. А. Диференціальна геометрія і топологія: Навч. посібник для студ. — Харків : Основа, 1995. — 304 с. — ISBN 5-7768-0388-8.