Вершина кривої

В геометрії кривих, вершина — це точка, в якої перша похідна кривини дорівнює нулю.[1] Як правило, це локальний максимум або мінімум кривини,[2] і деякі автори визначають вершину як екстремальну точку кривини.[3] Однак, тут можуть виникнути спеціальні випадки, наприклад, коли друга похідна теж дорівнює нулю або коли кривина постійна.

Еліпс (червоний) та його еволюта (синя). Точки є вершинами кривої та кожна з них відповідає вістрю еволюти.

Приклади

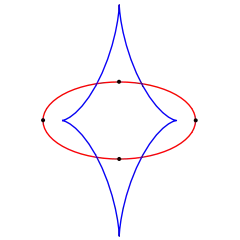
Гіпербола має дві вершини, на кожній гілці — одну. Ці вершини мають найменшу відстань поміж двома точками на гіперболі та лежать на головній осі. На параболі всього одна вершина, і вона лежить на осі симетрії.[2] В еліпса чотири вершини, дві з них лежать на великій осі та дві на малій.[4]

На колі, оскільки воно має сталу кривину, будь-яка точка є вершиною.

Точки перегину и дотику

Вершини — це точки, де крива має дотик порядку 3 зі стичним колом в цій точці.[5][6] Звичайно точки на кривій мають зі стичним колом дотик другого порядку. Еволюта кривої звичайно має касп, якщо крива має вершину[6]. Бувають й інші особливі точки в вершинах великого порядку, в яких порядок дотику зі стичним колом більше трьох.[5] Хоча звичайно крива не має вершин високого порядку, у сімействах кривих дві звичайні вершини можуть злитися в вершину великого порядку, а потім зникнути.

Множина симетрії кривої має кінці в каспах, що відповідають вершинам, а срединна вісь, підмножина множини симетрії, також має кінці в каспах.

Інші властивості

Згідно з теоремою про чотири вершини будь-яка проста замкнена пласка крива повинна мати щонайменше чотири вершини.[7] Більш загальне твердження, що будь-яка проста замкнена крива у просторі розташована на опуклій поверхні, або обмежує локально опуклий диск, має чотири вершини[8][9].

Якщо крива дзеркально симетрична, вона має вершину в точці перетину осі симетрії з кривою. Таким чином, поняття вершини кривої тісно пов'язано з оптичними точками, точками, в яких оптична вісь перетинає поверхню лінзи.

Примітки
  1. Agoston, 2005, стор. 570; Gibson, 2001, стор. 126.
  2. Gibson, 2001, стор. 127.
  3. Fuks & Tabachnikov, 2007, стор. 141.
  4. Agoston, 2005, стор. 570; Gibson, 2001, стор. 127.
  5. Gibson, 2001, стор. 126.
  6. Fuks & Tabachnikov, 2007, стр. 142.
  7. Agoston, 2005, Теорема 9.3.9, стор. 570; Gibson, 2001, Section 9.3, «The Four Vertex Theorem», стор. 133–136; Fuks & Tabachnikov, 2007, Теорема 10.3, стор. 149.
  8. Sedykh, V.D. (1994). Four vertices of a convex space curve. Bull. London Math. Soc. 26 (2): 177–180.
  9. Ghomi, Mohammad (2015). Boundary torsion and convex caps of locally convex surfaces. arXiv:1501.07626.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.