Теорія фільтрації

Основне співвідношення теорії фільтрації — закон фільтрації — встановлює зв'язок між швидкістю фільтрації (або витратами) і ґрадієнтом тиску, який спричиняє фільтраційний рух. Розглядають закони фільтрації при ламінарному русі рідини - це закон Дарсі і турбулентному - в цьому випадку швидкість фільтрації визначається за рівнянням Шезi – Краснопольського[1].

Водопроникність гірських порід характеризується коефіцієнтом фільтрації, коефіцієнтом швидкості руху води у порах й тріщинах та величиною питомого поглинання. Коефіцієнт фільтрації ${\displaystyle K}$ представляє собою швидкість фільтрації при гідравлічному градієнті, рівному одиниці. За законом Дарсі

${\displaystyle K={\frac {V}{I}}={\frac {Q}{FI}}.}$

За градієнту ${\displaystyle I=1,}$

${\displaystyle K=V={\frac {Q}{F}},}$

де ${\displaystyle V}$ — швидкість фільтрації, ${\displaystyle Q}$ — витрата потоку, ${\displaystyle F}$ — площина поперечного перетину потоку. Відповідно, коефіцієнт фільтрації інакше можна визначити як фільтраційну витрату, віднесену до одиниці площини поперечного перетину потоку при гладієнті, рівному одиниці. Коефіцієнтом швидкості фільтрації ${\displaystyle K_{0}}$ називається швидкість руху води у порах або тріщинах за гідравлічного градієнту, рівного одиниці

${\displaystyle K_{0}={\frac {V}{P_{0}}}={\frac {Q}{P_{0}F}},}$

де ${\displaystyle P_{0}}$ — пористість (скажність) порід. Таким чином, коефіцієнт швидкості фільтрації є витратою підземного потоку, віднесений до одиниці площини поперечного перерізу лише пор та тріщин у породі.

Найменші пустоти мають таку властивість, що сили молекулярної взаємодії між рідиною й твердими стінками є дуже великими. Вони утворюють молекулярні пори. У найбільших пустотах взаємодія рідини із стінками лише частково впливає на її рух. Такі пустоти називаються кавернами. Проміжне місце між молекулярними порами та кавернами займають просто пори. Тверде тіло, яке містить пори, представляє собою пористе середовище: пісок, пісковик, вапняк.

Газ, рідину, суміш рідини та газу, іншими словами — текуче середовище, часто називають збірним терміном флюїд (fluid), якщо не ставиться задача виділити характерні особливості руху даного середовища.

Якщо процеси у області фільтрації й розподілу щільності флюїдів у ній задані, то поле швидкостей фільтрації описується системою рівнянь (крайовою задачею):

${\displaystyle {\begin{cases}\mathrm {div} \,\rho {\textbf {v}}+{\frac {\partial \rho m}{\partial t}}+G=0;\\p(\Gamma _{1})=0;\\v_{n}(\Gamma _{2})=v_{\Gamma }.\end{cases}}}$

Тут ${\displaystyle \rho }$ — густина флюїду, ${\displaystyle {\textbf {v}}}$ — швидкість фільтрації, ${\displaystyle m}$ — пористість породи, ${\displaystyle t}$ — час, ${\displaystyle G}$ — інтенсивність генерації й поглинання флюїду, ${\displaystyle p}$ — тиск флюїду, ${\displaystyle v_{n}}$ — нормально до межі області компоненту швидкості фільтрації. Перше рівняння системи описує баланс маси флюїду у одиничному об'ємі фільтруючої породи, два наступних рівняння — умови на межах згори ${\displaystyle \Gamma _{1}}$ та знизу — збоку ${\displaystyle \Gamma _{2}.}$ Друге рівняння записане для випадку, коли верхньою межою ${\displaystyle \Gamma _{1}}$ є поверхня Землі або, точніше, дзеркало ґрунтових вод. Межу ${\displaystyle \Gamma _{2}}$ обирають, як правило, таким чином, щоб нормальна їй швидкість фільтрації ${\displaystyle v_{n}}$ була рівною нулю (точніше, щоб її можна було вважати рівною нулю в межах припустимих похибок), тобто щоб не було перетоку через межу розглядуваного об'єму із суміжними йому об'ємам.

Поле швидкостей фільтрації та поле тиску пов'язані, оскільки градієнт тиску є одним з компонентів сили, яка викликає фільтрацію. Наприклад, для ньютонівської рідини

${\displaystyle {\textbf {v}}=(K/\mu )(-\nabla \varrho +\rho g),}$

де ${\displaystyle K}$ — проникність породи, ${\displaystyle \mu }$ — в'язкість флюїду. Для рішення вищенаведеної системи рівнянь до першого рівняння замість швидкості підставляють цей вираз замість швидкості, і задача про рух флюїду переводиться у задачу про розподіл тиску (або напору у випадку потенційної течії):

${\displaystyle {\begin{cases}\mathrm {div} [(\rho K/\mu )(-\nabla p+\rho g)]+{\frac {\partial \rho m}{\partial t}}+G=0;\\p(\Gamma _{1})=0;\\{\frac {\partial p}{\partial n}}(\Gamma _{2})=\varphi {\Gamma _{2}}.\end{cases}}}$

Таким чином, математично задача про поле швидкостей фільтрації є задачею про поле його тиску[2].

Якщо всередині твердого тіла виникли тріщини, таке тіло представляє собою приклад тріщинуватого середовища. Розтрісканість гірської породи макротріщинами й мікротріщинами, які не зміщують шари порід одна відносно одної, можна об'єднати під терміном «тріщинуватість».

Рух текучого середовища через пори або тріщини можливий, якщо декотрі з пор або тріщин кореспондуються між собою. Флюїд, який заповнює кореспондовані пори або тріщини, утворює неперервне середовище (континуум), який займає деяку частину усього простору, який належить об'єму пористого або тріщинуватого середовища. Надзвичайно малі розміри порових каналів, їх неправильна форма, велика поверхня шорстких стінок — усе це створює великі опори руху рідини та газу. Цей опір є головною причиною дуже низької швидкості переміщення рідини й газу у пористому середовищі; швидкості у процесі фільтрації виявляються значно нижчими, ніж швидкості руху у трубах або відкритих руслах.

Через те, що порові канали мають неправильну форму й різноманітні розміри, неможливо дослідити рух частинок рідини або газу по усій множині каналів; неможливо точно знати форми й розміри кожного з цієї множини каналів, які перерізають товщу реальної пористої породи. Тому спочатку розвитку теорії фільтрації пішли по шляху побудови спрощених моделей реального пористого середовища. Припустимо, що пористе середовище недеформівне. Оскільки рух в'язкої рідини добре досліджений у трубах циліндричної форми, приймають, наприклад, усі пори циліндричними. Модель пористого середовища, побудована на основі припущення, що усі пори — вузькі циліндри, розташовані паралельно один до одного, називається моделлю ідеального ґрунту.

Інша модель пористого середовища у вигляді множини кулеподібних частинок однакового діаметру є модель фіктивного ґрунту.

Фіктивний ґрунт може моделювати добре відсортований пісок із правильним пакуванням зерен. Однак навіть за впорядкованого пакування зерен для природних сипучих матеріалів виявляється наступна закономірність: чим менший розмір зерен, тим більшою є пористість. Для природних й штучних матеріалів розрізняють дві пористості: загальну, або абсолютну пористість й активну, або ефективну пористість.

Об'єм порового простору такого природного матеріалу, як пісок, змінюється незначно навіть під дією високих тисків. Можна вважати, що пористість цих твердих матеріалів мало змінюється за мінливих тисків. Але пористість, наприклад, глини, є досить сприйнятливою до тиску: она значно зменшується із збільшенням глибини залягання під поверхнею землі. Залежність пористості глини із глибиною ${\displaystyle z}$ представляється формулою:

${\displaystyle m=m_{0}\theta ^{-az},}$

де ${\displaystyle m_{0}}$ — середня пористість поверхневих глин, ${\displaystyle a}$ — стала. За значень ${\displaystyle m_{0}}$ 0,4-0,5 пористість глиняного сланця на глибині 1800 м оцінюється величиною ${\displaystyle m=0,05.}$

На пониження значення пористості гірських порід разом із стисненням впливає їх зцементованість. В'яжуча речовини, яка переважно розташовується у місцях колишніх контактів між зернами осадкових порід, утворилася протягом геологічного періоду.

Зразок пористого середовища

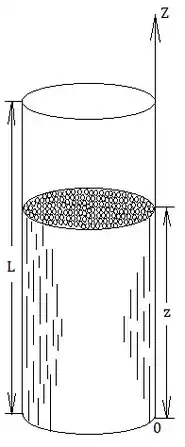
Для практичних розрахунків необхідно знати середню просвітність декотрого об'єму пористого середовища. Нехай маємо зразок циліндричної форми (такий зразок, вилучений зі свердловини, називається керном). Площа пор у перетині циліндру на відстані ${\displaystyle z}$ від його основи виражається у функції координати ${\displaystyle z}$, тобто ${\displaystyle F_{1}(z).}$ Довжина зразка дорівнює ${\displaystyle L.}$ Нехай просвітність у цьому перетині циліндру

${\displaystyle m'(z)={\frac {F_{1}(z)}{F}},}$

де ${\displaystyle F}$ — площа основи циліндру.

Середнє значення просвітності ${\displaystyle {\bar {m}}'}$ визначиться як

${\displaystyle {\bar {m}}'={\frac {1}{L}}\int _{0}^{L}m'(z)dz.}$

Але об'єм розглядуваного циліндру ${\displaystyle \tau =LF,}$ а об'єм пор у даному зразку

${\displaystyle \tau _{\text{п}}=\int _{0}^{L}F_{1}(z)dz.}$

Відповідно,

${\displaystyle {\bar {m}}'={\frac {1}{LF}}\int _{0}^{L}m'(z)Fdz={\frac {1}{\tau _{0}}}\int _{0}^{L}F_{1}(z)dz={\frac {\tau _{\text{п}}}{\tau }}=m.}$

Таким чином, середня просвітність дорівнює пористості ${\displaystyle m.}$[3]

У природі геохемічні процеси є сукупністю хемічних реакцій, які перебігають у земній корі при фільтрації й дифузії мінералоутворювальних розчинів. Особливе значення мають гетерохімічні реакції, які пробігають на рухомих фізико-хімічних бар'єрах. Динаміка хемічної взаємодії між розчином й твердим пористим тілом за дифузії через застійні порові розчини виражається наступною формулою:

${\displaystyle A_{\text{рід}}+B_{\text{тв}}=E_{\text{тв}}.}$

У випадку одновимірної дифузії по напрямку осі ${\displaystyle x,}$ яка супроводжується незворотною реакцією першого порядку, система рівнянь матеріального балансу речовини ${\displaystyle A_{\text{рід}}}$ й кінетики реакції має вигляд[4]

${\displaystyle {\begin{cases}{\frac {\partial q}{\partial t}}+{\frac {\partial C}{\partial t}}=D{\frac {\partial ^{2}C}{\partial x^{2}}},\\{\frac {\partial q}{\partial t}}=kC,\quad (q\leq q_{0}).\end{cases}}}$

Тут ${\displaystyle q_{0}}$ — концентрація твердого продукту реакції (${\displaystyle E}$), яка відповідає повному заміщенню ${\displaystyle B}$ на ${\displaystyle E}$ (усі концентрації виражається у г${\displaystyle \cdot }$екв на см³ пористого середовища). Звичайно, концентрація ${\displaystyle q}$ не може перевищувати ${\displaystyle q_{0}.}$

Комірка Сліхтера

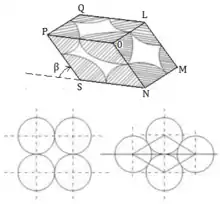
По ідеї Ч. Сліхтера, усі кулеподібні частинки, утворюючи дане пористе середовище, упаковані у всьому його об'ємі однаковим чином по елементам з восьми куль. Найменш щільне пакування куль — та, за якої центри восьми куль поміщаються у вершинах куба.

Найщільніше пакування отримується за розташування центрів восьми куль у вершинах ромбоедру із кутом ромбу ${\displaystyle \alpha =60^{o}.}$

Нехай маємо елементарну комірку Сліхтера. За будь-якого значення ${\displaystyle \beta }$ об'єм твердої фази ${\displaystyle V_{T}}$ у кожній комірці буде дорівнювати об'єму сферичної частинки:

${\displaystyle V_{T}=\pi d^{3}/6,}$

де ${\displaystyle d}$ — діаметр сфери. Звідси слідує, що пористість моделі ${\displaystyle m}$ повинна визначатися формулою

${\displaystyle m=1-\pi d^{3}/(6V_{0}),}$

де ${\displaystyle V_{0}}$ — об'єм ромбоедру. Але з наведеного малюнку слідує, що

${\displaystyle V_{0}=hS_{0}}$

та ${\displaystyle S_{0}=d^{2}\sin \beta ,}$

де ${\displaystyle h}$ — висота ромбоедру, ${\displaystyle S_{0}}$ — площина його основи. Таким чином,

${\displaystyle m=1-\pi d/(6h\sin \beta ),}$

і задача зводиться до визначення ${\displaystyle h.}$ Легко порахувати, що якщо кут ${\displaystyle \beta }$ буде змінюватися у межах від 60 до 90 градусів, то пористість моделі Сліхтера буде змінюватися у межах від 0,259 до 0,476. Таким чином вдається для гранулярної моделі пов'язати пористість із основною та єдиною характеристикою геометрії пор — кутом ${\displaystyle \beta }$.

Для аналізу руху рідини всередині комірки уводиться у розгляд просвітність ${\displaystyle n,}$ яка визначається співвідношенням площини просвіту ${\displaystyle S}$ між кулями у площині, яка сполучає їхні центри, до площини основи ромбоедру ${\displaystyle S_{0}:}$

${\displaystyle n=S/S_{0}.}$

Оскільки площина просвіту дорівнює площині ${\displaystyle S_{0}}$ із відніманням площини кола, радіус якого дорівнює площині сфери, то:

${\displaystyle n={\frac {d^{2}\sin \beta -\pi d^{2}/4}{d^{2}\sin \beta }},}$

звідки

${\displaystyle n=1-\pi /(4\sin \beta ).}$

Для вивчення течії рідини у моделі Ч.Сліхтер розглядав спочатку частковий випадок найтіснішого розташування сферичних частинок у пакуванні (${\displaystyle \beta =60^{o}}$). У цьому випадку у кожній комірці моделі існуватимуть два фільтраційних канали, форма перетину яких представляє собою криволінійні трикутники із змінюваними по довжині комірки розмірами. Обидва ці канали замінюються каналом сталого перетину ${\displaystyle {\bar {S}},}$ який має форму рівностороннього трикутника. Середня швидкість течії ${\displaystyle {\bar {\textbf {v}}}_{1}}$ визначається формулою

${\displaystyle {\bar {\textbf {v}}}_{1}={\frac {\bar {S}}{20{\sqrt {3}}\mu }}-{\frac {\Delta p}{l}},}$

де ${\displaystyle \mu }$ — фізична в'язкість рідини, ${\displaystyle l}$ — довжина каналу, ${\displaystyle \Delta p}$ — перепад тиску на кінцях каналу. Таким чином, задача зводиться до визначення ${\displaystyle {\bar {S}}}$ та ${\displaystyle l.}$ Рішення цієї задачі С. Сліхтером полягає у тому, що шляхом геометричних перетворень він пов'язує довжину ${\displaystyle l}$ із діаметром сферичної частинки ${\displaystyle d,}$ а площу ${\displaystyle {\bar {S}}}$ — із просвітністю:

${\displaystyle l=1,065d;}$

${\displaystyle {\bar {S}}=1,436nS_{0}.}$

Підставляючи ці формули, знаходимо

${\displaystyle {\bar {\textbf {v}}}_{1}={\frac {1,436}{20{\sqrt {3}}\cdot 1,065}}{\frac {nS_{0}}{\mu }}{\frac {\Delta p}{d}}.}$

Із похибкою ${\displaystyle \approx 2\%}$

${\displaystyle 1,436/(20{\sqrt {r}}\cdot 1,065)=1/(8\pi ),}$

то

${\displaystyle {\bar {\textbf {v}}}_{1}={\frac {nS_{0}}{n\pi \mu }}{\frac {\Delta p}{d}}.}$

За висоти ромбоедру, яка визначається за формулою ${\displaystyle h=d\sin \alpha ={\frac {d\sin \beta }{1+\cos \beta }}{\sqrt {1+2\cos \beta }},}$ отрмуємо

${\displaystyle {\bar {\textbf {v}}}={\frac {nd^{2}\sin ^{2}\beta {\sqrt {1+2\cos \beta }}}{16\pi \mu (1+\cos \beta )}}{\frac {\Delta p}{h}},}$

де ${\displaystyle {\bar {\textbf {v}}}={\bar {\textbf {v}}}_{1}/2.}$ Виключивши вирази тригонометричних функцій (вважаючи, що ${\displaystyle \sin ^{2}\beta =(1-\cos \beta )(1+\cos \beta )}$), отримується відома формула Сліхтера:

${\displaystyle {\bar {\textbf {v}}}={\frac {d^{2}}{96h}}{\frac {n}{(1-m)}}{\frac {\Delta p}{h}}.}$ Порівнюючи цей вираз із формулою закону Дарсі ${\displaystyle {\bar {\textbf {v}}}={\frac {k}{\mu }}{\frac {\Delta p}{h}},}$ знайдемо

${\displaystyle k=d^{2}n/[96(1-m)],}$

де ${\displaystyle k}$ — проникність моделі[5].

• Леонтьев Н.Е. Основы теории фильтрации. — М.: Изд-во ЦПИ при механико-математическом факультете МГУ, 2009. — С. 24–29. — 88 с.
• Р.Д. Канаевская - Математическое моделирование гидродинамических процессов разработки месторождений углеводородов, с.106.