Суцільне середовище
Суці́льне середо́вище (англ. continuous medium, англ. continuum; нім. Kontinuität f) — фізична система з нескінченним числом внутрішніх ступенів свободи.
| Механіка суцільних середовищ |
|---|
 |
|
Тверде тіло:
Напруження • Деформація • Теорія малих деформацій • Теорія великих деформацій • Теорія пружності • Механіка контактної взаємодії • Опір матеріалів • Теорія пластичності • Механіка руйнування |
|
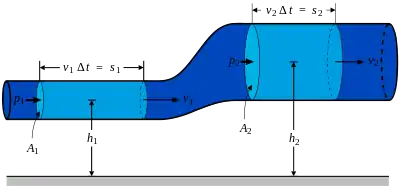
Флюїд: Тиск • Гідростатика (закон Архімеда; закон Паскаля) • Гідродинаміка (закон Бернуллі) • В'язкість (ньютонівська рідина; неньютонівська рідина) Рідина: Поверхневий натяг • Капілярний ефект |
|
В'язкоеластичність • Розумні рідини (Магнетореологічна рідина, Електрореологічна рідина, Феромагнітна рідина) • Реометрія |
|
Основні рівняння |
Загальний опис
Класична механіка розглядає рух механічних систем із скінченим числом ступенів свободи. Наприклад, абсолютно тверде тіло, що складається з довільної кількості частинок, є системою з шістьма ступенями свободи. Якщо брати до уваги рухи деформації, то тіло може розглядатися як система рухомих частинок або як суцільне середовище із втратою при цьому частини інформації про рухи окремих частинок тіла. Для довільного реального середовища, яке містить у собі сумірну з числом Авогадро кількість атомів чи молекул, немає ніякого сенсу розглядати систему 1023 диференціальних рівнянь руху з відповідною кількістю початкових умов.
Використання тієї чи іншої моделі суцільного середовища дозволяє спростити задачу за рахунок усереднення частини процесів, які відбуваються у середовищі. Іншими словами, замість розгляду рухів окремих атомів чи молекул, у моделях суцільного середовища частина простору, що заповнена середовищем, наділяється скалярними, векторними та тензорними характеристиками — полями (функціями координат та часу).
Рух суцільного середовища в просторі, на відміну від інших механічних систем, описується не координатами і швидкостями окремих частинок, а скалярним полем густини і векторним полем швидкостей. Залежно від завдань, до цих полів можуть додаватися поля інших фізичних величин (концентрація, температура, поляризація тощо). Якщо серед характеристик середовища зустрічаються тензорні величини, відповідні рівняння для суцільного середовища записують у тензорній формі.
Суцільне середовище — ідеалізоване (уявне) середовище, вивчення макроскопічних процесів в якому здійснюється без урахування молекулярної будови. Таке уявлення не суперечить фізичним даним, оскільки, наприклад, кубик повітря зі стороною 1 мкм містить 2,7•107 молекул. Такі елементи об'єму можна вважати фізично безмежно малими. Це уявлення дає змогу при дослідженні використовувати апарат неперервних функцій, диференціальне та інтегральне числення.
Рух суцільного середовища представляє собою другий закон Н'ютона, записаний для елементарного об'єму. Нехай елементарний об'єм представляє собою паралелепіпед маси із гранями Другий закон Н'ютона для нього буде мати вигляд:
де - швидкість, - щільність, - вектор результуючої сили, яка діє на об'єм. Які сили діють на елементарний об'єм рідини? Сили можна поділити на поверхневі та об'ємні. До об'ємних сил відносяться сили тяжіння, електричні, магнітні сили тощо. Поверхневі сили можна представити у вигляді тензора напруг:
де головна діагональ (символ Кронекера ) - нормальні напруги (тобто вони спрямовані по нормалі до поверхні). Усі інші напруги - дотичні (спрямовані по дотичній). Причому
Рівняння нерозривності (суцільності) називають також рівнянням збереження маси. Нехай існує об'єм , обмежений поверхнею Маса може змінитися лише за рахунок втікаючого й витікаючого з нього потоку рідини.
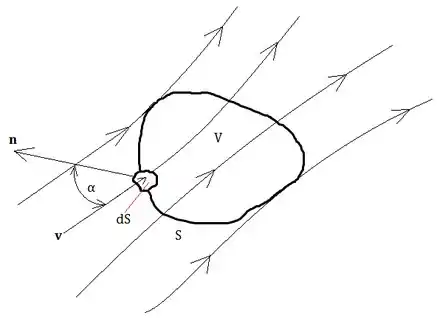
У такому випадку швидкість зміни маси у об'ємі дорівнює потоку (витраті) рідини через даний об'єм. Витрата рідини із щільністю , яка протікає із швидкістю через перетин обчислюється за формулою Тоді потік через елемент площини буде дорівнювати Інтегруючи по поверхні отримуємо:
Враховуючи, що
За формулою Остроградського-Гауса
Інтеграл по довільному об'ємові від функції може дорівнювати нулю лише якщо сама функція дорівнює нулю. Звідси випливає рівняння суцільності
У тензорних позначеннях воно має вигляд
Див. також
Посилання
Література
- Седов Л. И. Механика сплошной среды. Том 1. — М.: Наука, 1970. — 492 с.
- Мала гірнича енциклопедія : у 3 т. / за ред. В. С. Білецького. — Д. : Східний видавничий дім, 2013. — Т. 3 : С — Я. — 644 с.
- Бойко В. С., Бойко Р. В. Тлумачно-термінологічний словник-довідник з нафти і газу. Тт. 1-2, 2004—2006 рр. 560 + 800 с.
