Формула Гауса — Бонне
Формула Гауса—Бонне пов'язує Ейлерову характеристику області двовимірного многовида з кривиною Гауса в цій області та геодезичною кривиною кривої, яка обмежує область.
Формулювання
Нехай — компактний двовимірний орієнтований ріманів многовид з гладкою межею . Позначимо через гаусову кривину та через геодезичну кривину . Тоді
де — ейлерова характеристика .
Зокрема, якщо у межа відсутня, отримуємо спрощений вираз
Якщо поверхня деформується, то її ейлерова характеристика не змінюється, в той час як гаусова кривина може змінюватися в кожній точці. Проте, згідно з формулою Гауса-Бонне, інтеграл гаусової кривини залишається не змінним.
Пояснення позначень
Топологія областей інтегрування
Область обмежена. Але вона може бути доволі складною, мати одну або кілька компонент зв'язності:
Очевидно, що при цьому перший інтеграл в формулі (1) розбивається на суму інтегралів по компонентах. Кожна з цих компонент в свою чергу може бути топологічно складною.
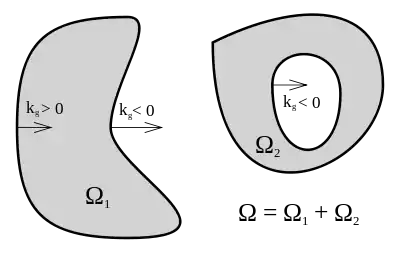
Зокрема область може повністю покривати замкнутий многовид (наприклад сферу, тор, …) і не мати межі зовсім — тоді другого інтеграла в формулі (1) не буде:
В інших випадках межа області може складатися з одного контуру (наприклад якщо область гомеоморфна кругу), або більшої кількості контурів (наприклад якщо область є кільцем між двома концентричними колами):
В цих випадках інтеграл по межі також розбивається на суму інтегралів по .
Кривини
Буквою під першим інтегралом (1) позначено кривиною Гауса другого степеня, яка для двовимірного многовида дорівнює половині скалярної кривини:
Геодезична кривина кривої взагалі кажучи є вектором, ортогональним до одиничного дотичного вектора , і який лежить у многовиді. Але в формулі (1) через позначено скалярну величину — проекцію вектора геодезичної кривини на напрям нормалі, напрямленої всередину області .
Запишемо вищесказане математично. Компоненти вектора геодезичної кривини обчислюються через тензорну похідну одиничного дотичного вектора по натуральному параметру кривої:
Нормаль до вектора можна утворити дією одиничного антисиметричного тензора , а тому (при належному виборі напрямку обходу контуру):
Коефіцієнт в правій частині формули (7) той самий, який стоїть під другим інтегралом в формулі (1).
Злами на контурах
В попередньому підпункті ми розглядали гладкий контур . Але неважко, використовуючи граничний перехід, узагальнити формулу (1) для кусково-гладкої межі яка складається з гладких дуг, що сходяться під деяким кутом між собою (дивіться наприклад статтю Геодезичний трикутник). Якщо в точці зламу дотичний вектор розвертається на кут в сторону області (може бути додатне чи від'ємне число) то формула (1) узагальнюється до такої:
В цій формулі другий інтеграл береться по гладких ділянках дуг межі .
Для виводу формули (8) область , яка має злами на межі, треба апроксимувати областю , яка має згладжені кути. Потім радіус закруглення на кутах спрямовуємо до нуля.
Ейлерова характеристика
Обмежену двовимірну область можна розбити лініями на кілька менших підобластей , гомеоморфних кругу. Лінії в свою чергу можна поділити точками на дуги, гомеоморфні відрізку. Якщо позначити кількість точок буквою (вершини графу), кількість дуг буквою (ребра графу), а кількість підобластей буквою (грані), то наступне ціле число:
не залежить від способу розбивки області і називається характеристикою Ейлера. Для кожної підобласті можна знайти карту (систему координат ), яка відображає область Евклідової площини в .
Три етапи доведення теореми Гауса-Бонне
На першому етапі доводимо теорему для простої області, гомеоморфної кругу, з гладкою границею. На другому етапі граничним переходом поширюємо теорему на просту область з кутами. На третьому (топологічному) етапі об'єднуємо та склеюємо прості області в довільну область і показуємо, що при операціях об'єднання та склейки формула (1) залишається справедливою.
Перший етап доведення
Обчислення характеристики Ейлера
Обчислимо характеристику Ейлера для простої області . Межа цієї області є контуром , гомеоморфним колу. Поставимо на цьому контурі дві точки і , які розбивають наш контур на дві дуги, гомеоморфні відрізку. Маємо дві вершини, два ребра і одну грань — саму область , тому за формулою (9) маємо:
і нам треба довести наступну формулу для цього випадку:
Вектори на контурі
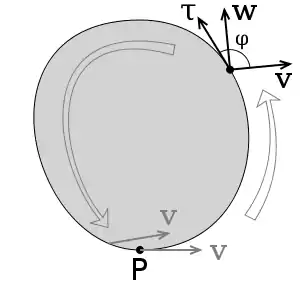
Візьмемо точку на контурі . Позначимо буквою вектор нормалі до контуру, напрямлений всередину області . При належному виборі напрямку обходу контуру компоненти цього вектора виражаються через дотичний вектор та одиничний антисиметричний тензор :
При обході контуру, очевидно, вектори і повернуться на кут і збіжаться з початковими значеннями цих векторів.
Щоб простежити, як здійснюється цей поворот, розглянемо паралельне перенесення векторів. Як відомо, при паралельному перенесенні двох векторів зберігаються довжини векторів і кут між ними. Нехай вектори і збігаються з векторами і в початковій точці , але потім при обході контуру переносяться паралельно і після обходу виявляються повернутими на деякий кут . Ці два вектора утворюють ортонормований базис:
Розкладемо одиничний дотичний вектор за базисом :
де — кут, на який повернутий вектор відносно вектора . На початку обходу . В кінці обходу вектор повернеться на кут , а вектор на кут , тому:
Повороти векторів на контурі і геодезична кривина
Маємо такі тензорні диференціали векторів вздовж контуру:
тому при диференціюванні рівності (15) одержуємо:
Порівнюючи формули (20) і (7) знаходимо:
Порівнюючи формули (22) і (11) одержуємо таку формулу, яку нам лишається довести:
Застосування формули Остроградського-Гауса
В лівій частині формули (23) стоїть інтеграл по двовимірній області , а в правій — поворот вектора при паралельному перенесенні довкола межі області , який природно буде виразити через контурний інтеграл. Ці два інтеграла — інтеграл по двовимірній області і інтеграл по межі цієї області можна пов'язати через застосування формули Остроградського-Гауса. Але для цього нам знадобиться допоміжне векторне поле, яке визначене і диференційовне скрізь всередині області та на її межі .
Вибір допоміжного векторного поля
Оскільки на контурі нас можуть цікавити лише кути між векторами а не їхні довжини, то доцільно вибрати допоміжне векторне поле одиничної довжини, причому не лише на контурі, а і скрізь всередині області :
Очевидно що умова (24) разом з неперервністю поля накладає деякі обмеження — це поле не може мати всередині точок завихрення або точок, із яких вектори розходяться (або навпаки, сходяться) в різні боки. В усьому іншому поле досить довільне.
Наприклад (хоч і необов'язково) можна взяти вектор напрямлений вздовж одного з координатних векторів. Коваріантні координати цього вектора:
Обчислення повороту вектора при паралельному перенесенні по контуру

На контурі розкладемо одиничний вектор по базису :
Тут вектори і ті ж самі що і раніше в цій статті — здійснюють паралельний обхід контуру. Кут між векторами є функцією від натурального параметра на контурі :
Оскільки при обході контуру вектор не змінює напрямку, а вектор повертається на кут то:
Знак мінус в цій формулі виник внаслідок того, що повертається сам базис, відносно якого ми міряємо .
Продиференціюємо формулу (26) вздовж кривої :
Тензорний диференціал вектора можна записати через коваріантну похідну:
Права ж частина формули (29) виражається через вектор:
який є одиничним вектором, повернутим на кут щодо вектора .
Одержання контурного інтеграла
Підставивши (30) і (31) в формулу (29), ми одержимо векторне рівняння:
в якому нас цікавить скалярна функція . Помножимо (32) скалярно на одиничний вектор і візьмемо інтеграл:
Інтеграл в лівій частині цієї рівності фактично є інтегралом по контуру. Для застосування формули Остроградського-Гауса нам потрібно, щоб підінтегральний вираз був скалярним добутком деякого вектора на вектор зовнішньої нормалі (в наших старих позначеннях це ).
Фактичне застосування формули Остроградського-Гауса
Домножимо рівняння (12) на , після цього знайдемо дотичний вектор :
і підставити його в підінтегральний вираз формули (33), одночасно перейменовуючи індекси:
Вираз у дужках в правій частині цього рівняння і буде тим вектором :
який підставляємо в рівняння (33):
Інтеграл являє собою потік вектора всередину контуру , враховуючи наш вибір напрямку нормалі . Застосовуючи формулу Остроградського-Гауса (і враховуючи знак) маємо інтеграл від дивергенції:
Завершення обчислень
Порівнюючи формули (38) і (23) ми бачимо що для завершення першого етапу нам досить перевірити рівність підінтегральних виразів цих формул:
Дивергенція вектора (36) розкладається на два доданка:
Розпочнемо з другого доданку, а ще краще з частини цього доданку окрім множника . Оскільки тензор антисиметричний, то:
Тензор Рімана для двовимірного многовида можна виразити через кривину Гауса K:
Тому вираз (41) спрощується:
а отже другий доданок формули (40) просто дорівнює Гаусовій кривині:
Залишається показати, що перший доданок формули (40) дорівнює нулю.
Це прямо слідує з того факту, що похідні одиничного двовимірного вектора факторизуються (розкладаються на множники):
Дійсно, підставляючи (46) в (45) одержимо вираз:
в якому скалярний добуток векторів в других дужках дорівнює нулю.
Нарешті покажемо справедливість розкладу (46). Із одиничності вектора слідує:
Оскільки вектор також ортогональний до то маємо наступну однорідну систему двох лінійних рівнянь з двома невідомими :
Ця система має ненульовий розв'язок, тому матриця її коефіцієнтів:
вироджена і рядки цієї матриці пропорційні. Тобто ми маємо друге рівняння (46). Перше рівняння одержується аналогічно.
Формулу (11) доведено.
Другий етап доведення
Розглянемо просту область з кусково-гладкою межею. Ми можемо згладити всі кути, вписуючи гладку дугу в кожен криволінійний кут (див. малюнок).
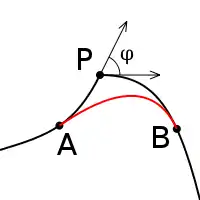
Одержуємо область з гладкою межею, до якої можна застосувати теорему Гауса-Бонне, доведену на першому етапі. Спробуємо здійснити граничний перехід формули (11) стягуючи дугу в точку зламу .
Перший інтеграл формули (11) для згладженої і незгладженої кривих, відрізняється на величину інтеграла по криволінійному трикутнику
Оскільки площа цього трикутника прямує до нуля, а Гаусова кривина обмежена, то і величина (51) прямує до нуля. Отже при граничному переході перший інтеграл
зберігає свій вигляд, просто область може мати злами на контурі.
З другим (контурним) інтегралом складніше. Розглянемо спочатку випадок плоского многовида (евклідову площину). В цьому разі паралельне перенесення не залежить від шляху і тому можна говорити про кут між векторами, що знаходяться в різних точках. Інтегрування геодезичної кривини по дузі , згідно з формулою (22), дає кут між дотичними в точках і :
При граничному переході ця величина прямує до кута між двома дотичними векторами в точці зламу :
а інтеграли по (викинутих при згладжуванні) дугах і прямують до нуля, оскільки геодезична кривина цих дуг залишається обмеженою, а їхня довжина зменшується до нуля.
Із формули (54) слідує формула (8) при , що і треба було довести.
Нам ще залишається довести, що формула (54) має місце і в загальному випадку викривленого многовида. Виберемо систему координат на многовиді в околі точки таку, що метричний тензор в точці записується одиничною матрицею , а символи Крістофеля в цій точці дорівнюють нулю.
Дану систему координат можна розглядати як дифеоморфне відображення між областю многовиду та областю площини (картою), в якій ця система координат є декартовою.
Позначимо елемент довжини кривої на карті:
а буквою з тильдою — геодезичну кривину кривої на карті. Тоді:
Крапками позначено похідні по параметру . Із двох останніх формул уже можна зробити висновок про однаковість, з точністю до нескінченно малих доданків, двох інтегралів від геодезичної кривини по дузі , один з яких береться по многовиду, а другий по карті:
але для цього потрібні два додаткових припущення щоб унеможливити надмірну довжину дуги за рахунок осциляцій або закручувань у спіраль. А саме, припустимо що знак геодезичної на дузі є постійний, а також, що дуга не має інших спільних точок з криволінійним кутом, окрім своїх кінців.
Дійсно, множник
прямує до одиниці, а символи Крістофеля до нуля внаслідок спеціального вибору системи координат. Отже і в загальному випадку справедлива границя (54), а тому для простої області доведено варіант формули (8):
Третій етап доведення
Розіб'ємо топологічно складну область на скінченну кількість простих підобластей , до кожної з яких можна застосувати формулу (58).
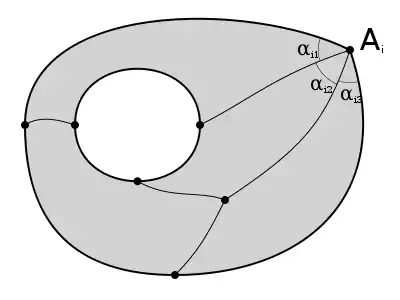
Характеристика Ейлера обчислюється за формулою (9)
де позначають кількості вершин, ребер та граней (підобластей ). Для простоти доведення будемо вважати всі ребра одержаного графу гладкими кривими, а всі злами на контурах відбуваються при вершинах графу. Зручно розглядати внутрішні кути при всіх вершинах графу. Тут перший індекс () нумерує всі вершини, як внутрішні, так і ті, що лежать на межі області . Другий індекс () нумерує кути при вершині . Злам при вершині є доповненням до внутрішнього кута:
і ми можемо знайти суму формул (58) для всіх підобластей :
Розберемося з кожним із трьох доданків у правій частині формули (59). Перший доданок, очевидно, дорівнює інтегралу по цілій області :
В другому доданку треба розрізняти зовнішні ребра , які лежать на межі, від внутрішніх. Інтегрування по внутрішньому ребру відбувається двічі, при розгляді двох суміжних підобластей, що розділяються даним ребром. Причому проекції геодезичної кривини будуть протилежними:
A отже всі інтеграли по внутрішніх ребрах взаємно компенсуються і в сумі (59) лишаються тільки інтеграли по зовнішніх ребрах:
Перейдемо до розгляду третього доданка формули (59). Для кожної внутрішньої вершини маємо:
де — кількість кінців (внутрішніх) ребер, що сходяться в цій вершині.
Для вершини на межі області маємо:
де також, як і в попередній формулі, позначає кількість кінців внутрішніх ребер, що сходяться у вершині , а позначає кут, на який повертається дотичний до лінії межі вектор при переході через точку .
Оскільки кожне ребро має два кінця, то сума всіх цих кінців дорівнює подвоєній кількості внутрішніх ребер:
і ми можемо записати для третього доданка:
Очевидно, що межа складається з декількох контурів, гомеомеорфних колу. На кожному такому контурі, а отже і на всій межі кількість вершин і кількість ребер однакова. Маємо:
Підставимо формули (60), (61), (65) і (66) в (59). Одержуємо:
що є еквівалентом формули (8). Теорему повністю доведено.
Історія
Приватний випадок цієї формули для геодезичних трикутників був отриманий Гаусом, проте він не опублікував її. В 1848 році її опублікував французький математик Бонне П'єр Осіян, який узагальнив формулу на випадок диска обмеженого довільною кривою. У сучасному формулюванні формула вперше з'являється у Вільгельма Бляшке.