Хіральний вузол

В теорії вузлів хіральний вузол — це вузол, який не еквівалентний своєму дзеркальному відображенню. Орієнтований вузол, еквівалентний своєму дзеркальному відображенню, називається амфіхіральним вузлом або ахіральним вузлом. Хіральність вузла є інваріантом вузла. Хіральність вузлів можна далі класифікувати в залежності від того, оборотний він чи ні.

Існує лише 5 типів симетрій вузлів, які визначаються хіральністю і оборотністю — повністю хіральний, оборотний, додатно амфіхіральний незворотний, від'ємно амфіхіральний незворотний і повністю амфіхіральний оборотний[1].

Історія питання

Хіральність деяких вузлів давно припускалась і доведена Максом Деном 1914 року. П. Г. Тет висловив гіпотезу, що всі амфіхіральні вузли мають парне число перетинів, але Морвен Тіслвейт 1998 року знайшов контрприклад[2]. Однак гіпотеза Тета доведена для простих альтернованих вузлів[3].

Число вузлів кожного виду хіральності для кожного числа перетинів
Число перетинів 3 4 5 6 7 8 9 10 11 12 13 14 15 16 OEIS sequence
Хіральні вузли 1 0 2 2 7 16 49 152 552 2118 9988 46698 253292 1387166 N / A
Двосторонні вузли 1 0 2 2 7 16 47 125 365 1015 3069 8813 26712 78717 A051769
Повністю хіральні вузли 0 0 0 0 0 0 2 27 187 1103 6919 37885 226580 1308449 A051766
Амфіхіральні вузли 0 1 0 1 0 5 0 13 0 58 0 274 1 1539 A052401
Додатно амфіхіральні вузли 0 0 0 0 0 0 0 0 0 1 0 6 0 65 A051767
Від'ємно амфіхіральні вузли 0 0 0 0 0 1 0 6 0 40 0 227 1 1361 A051768
Повністю амфіхіральніе вузли 0 1 0 1 0 4 0 7 0 17 0 41 0 113 A052400
  • Обидва можливих трилисники.
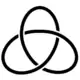  • Лівий трилисник.
  • Правий трилисник.

Найпростіший хіральний вузол — трилисник, хіральність якого показав Макс Ден. Всі торичні вузли хіральні. Многочлен Александера не може визначити хіральність вузла, а ось многочлен Джонса в деяких випадках може. Якщо V k (q) ≠ V k (q −1), то вузол хіральний, проте зворотне не обов'язково істинне. Многочлен HOMFLY ще краще розпізнає хіральність, але поки не відомо поліноміального інваріанта вузла, який би повністю визначав хіральність[4].

Двосторонній вузол

Оборотний хіральний вузол називається двостороннім. Один з прикладів двосторонніх вузлів — трилисник.

Повністю хіральний вузол

Якщо вузол не еквівалентний ні своєму оберненому, ні своєму дзеркальному образу, він називається повністю хіральним; приклад — вузол 9 32[5].

Амфіхіральний вузол
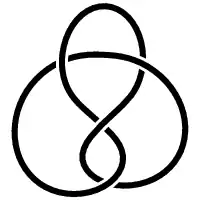
Вісімка є найпростішим амфіхіральним вузлом.

Амфіхіральний вузол— це вузол, який має автогомеоморфізм α 3-сфери, який обертає орієнтацію і фіксує вузол як множину.

Всі амфіхіральні альтерновані вузли мають парне число перетинів . Перший амфіхіральний вузол з непарним числом перетинів, а саме з 15 перетинами, знайшов Хосте (Hoste) та ін.[3]

Повна амфіхіральність

Якщо вузол ізотопний своєму оберненому і своєму дзеркальному образу, його називають повністю амфіхіральним. Найпростішим вузлом з цією властивістю є вісімка.

Додатна амфіхіральність

Якщо автогомеоморфізм α зберігає орієнтацію вузла, кажуть про додатну амфіхіральність. Це еквівалентно ізотопності вузла своєму дзеркальному відображенню. Жоден із вузлів з числом перетинів меншим від дванадцяти не є додатно амфіхіральним[5].

Від'ємна амфіхіральність
Перший від'ємно амфіхіральний вузол.

Якщо автогомеоморфізм α обертає орієнтацію вузла, кажуть про від'ємну амфіхіральність. Це еквівалентно ізотопності вузла оберненому дзеркальному відображенню. Вузол з цією властивістю з найменшим числом перетинів — це 817[5].

Примітки
  1. Hoste, Thistlethwaite, Weeks, 1998, с. 33—48.
  2. Jablan, Slavik & Sazdanovic, Radmila. «History of Knot Theory and Certain Applications of Knots and Links», LinKnot.
  3. Weisstein, Eric W. Amphichiral Knot(англ.) на сайті Wolfram MathWorld. Accessed: May 5, 2013.
  4. «Chirality of Knots 942 and 1071 and Chern-Simons Theory» by P. Ramadevi, T. R. Govindarajan, and R. K. Kaul
  5. Three Dimensional Invariants Knot Atlas

Література
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.