Чисельне диференціювання

Найпростішим методом є застосування скінченно-різницевих наближень. Всі різницеві формули отримують внаслідок розкладання функції в околі x в ряд Тейлора і виділення тільки кілька перших членів ряду.

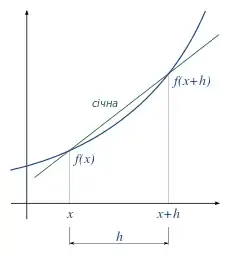
Простий метод оцінювання за допомогою двох точок полягає в обчисленні нахилу ближньої січної через точки (x,f(x)) та (x+h,f(x+h)). Оберемо маленьке число h, що являтиме невелику різницю двох значень x, та може бути як позитивним, так і негативним. Січна цієї лінії виглядатиме так: ${\displaystyle {f(x+h)-f(x) \over h}.}$

Цей вираз — Ньютонівський фактор різниці (також відомий як першорядна розділена різниця.)

Нахил цієї січної відрізняється від нахилу дотичної на величину, приблизно пропорційну h. При наближенні h до нуля, нахил січної наближується до нахилу дотичної. Отже, істиною похідною f в точці x є границя значення частки різниці, при наближенні січної до дотичної: ${\displaystyle f'(x)=\lim _{h\to 0}{f(x+h)-f(x) \over h}.}$

Чисельне диференціювання за допомогою класичних різницевих схем є погано обумовленою задачею. Для комплексної голоморфної функції, що має дійсні значення на дійсній осі, перша похідна може бути обчислена в околі x за допомогою формули в комплексній площині[1][2]

${\displaystyle f'(x)\approx \Im (f(x+ih))/h}$.

Ця формула є «наближенням похідної за допомогою комплексного кроку» з точністю порядку O(h²). Таке наближення похідної не має в собі операції різниці, як це відбувається в різницевих схемах. Тому ця формула має перевагу над формулами скінченних різниць в дійсній площині. При зменшенні кроку h чисельна похідна сходиться квадратично до точного значення і для будь-якого розміру кроку меншого 1e-8 досягає точності оцінки самої функції. Для кроку порядку точності комп'ютера для дійсних чисел формула гарантовано дає надзвичайно малу похибку на межі цієї точності.

Наведена вище формула справедлива тільки для обчислення похідної першого порядку. Як узагальнення для обчислення похідних будь-якого порядку використовують інтегральну формулу Коші.

${\displaystyle f^{(n)}(a)={n! \over 2\pi i}\oint _{\gamma }{f(z) \over (z-a)^{n+1}}\,\mathrm {d} z}$,

де інтегрування здійснюють чисельно.