Число перетинів графа

Нехай F — сімейство множин (дозволяється повторення множин в F. Тоді граф перетинів F — це неорієнтований граф, що має по вершині для кожного члена F і по ребру між будь-якими двома множинами, що мають непорожній перетин. Будь-який граф можна подати як граф перетинів[4]. Кількість перетинів графу — це найменше число k таке, що існує подання такого типу, для якого об'єднання множин F має k елементів[1]. Задача знаходження подання у вигляді графу перетинів із заданим числом елементів відома як задача знаходження базису графу перетинів[5].

Граф з числом перетинів чотири. Чотири виділені ділянки показують кліки, що покривають усі ребра графу.

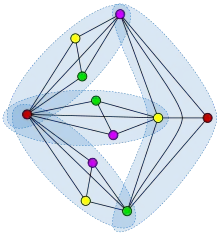
Альтернативне визначення числа перетинів графу G — це найменше число клік у G (повних підграфів графу G, які покривають усі ребра G[1][6]. Множина клік з такою властивістю називається покриттям ребер кліками, а тому число перетинів іноді називають числом покриття ребер кліками[7].

Рівність числа перетинів і числа покриття ребер кліками доводиться «прямолінійно». В одному напрямку, припустимо, що G є графом перетинів сімейства F множин, об'єднання U яких має k елементів. Тоді для будь-якого елемента x з U підмножина вершин графу G, відповідних множинам, що містять x, утворюють кліку — будь-які дві вершини цієї підмножини суміжні, оскільки відповідні їм множини мають непорожній перетин, що містить x. Далі — будь-яке ребро в G міститься в одній з таких клік, оскільки ребро відповідає непорожньому перетину, а перетин не порожній, якщо він містить принаймні один елемент U. Таким чином, ребра графу G можуть бути покриті k кліками, по одній для кожного елемента U. В іншому напрямку, якщо граф G можна покрити k кліками, то кожну вершина графу G можна подати множиною клік, що містять вершину[6].

Очевидно, що граф з m ребрами має число перетинів, яке не перевищує m — будь-яке ребро утворює кліку, і ці кліки разом покривають усі ребра[8].

Також правильно, що будь-який граф з n вершинами має число перетинів, яке не перевищує n²/4. Строгіше, ребра будь-якого графу з n вершинами можна поділити щонайбільше на n²/4 клік, які є або окремими ребрами, або трикутниками[2][6]. Це узагальнює теорему Мантеля, яка стверджує, що граф без трикутників має не більше n²/4 ребер. Для графів без трикутників оптимальне клікове покриття ребер має кліку для кожного ребра, а тому число перетинів дорівнює числу ребер[2].

Навіть сильніше обмеження можливе, якщо число ребер строго більше від n²/4. Нехай p дорівнює числу пар вершин, не з'єднаних ребрами заданого графу G і нехай t дорівнює числу, для якого t(t − 1) ≤ p < t(t + 1). Тоді число перетинів графу G не перевищує p + t[2][9].

Графи, які є доповненнями розріджених графів, мають невелике число перетинів: число перетинів будь-якого графу G з n вершинами не перевищує 2e²(d + 1)²ln n де e — основа натурального логарифма, d максимальний степінь додаткового графу G[10].

Перевірка, що у даного графу G число перетинів не перевищує заданого числа k є NP-повною задачею[5][11][12]. Таким чином, NP-складною задачею є обчислення числа перетинів заданого графу.

Задача обчислення числа перетинів, проте, є фіксовано-параметрично розв'язною. Тобто існує функція f така, що при рівності числа перетинів числу k час обчислення цього числа не перевищує добутку f(k) на поліном від n. Це можна показати, якщо звернути увагу на те, що існує не більше 2^k різних закритих околів у графі. Дві вершини, що належать одному і тому ж набору клік, мають одних і тих же сусідів, а тоді граф, утворений вибором однієї вершини для кожного закритого околу, має те саме число перетинів, що й початковий граф. Тому за поліноміальний час вхід можна звести до меншого ядра з максимум 2^k вершинами. Застосування алгоритму пошуку з поверненням з експоненційним часом роботи для цього ядра приводить до функції f яка є подвійною експонентою від k[13]. Подвійну експоненційну залежність від k не можна звести до простої експоненційної залежності за допомогою виділення ядра поліноміального розміру, поки поліноміальна ієрархія не зникне[14], і якщо гіпотеза про експоненційний час істинна, подвійної експонеційної залежності не уникнути, будемо ми використовувати виділення ядра чи ні[15].

Ефективніші алгоритми відомі для окремих класів графів. Число перетинів інтервального графу завжди дорівнює числу максимальних клік графу, яке можна обчислити за поліноміальний час[16][17]. Загальніше — кількість перетинів хордальних графів можна обчислити за алгоритмом, який будує порядок виключення вершин графу. На кожному кроці для кожної вершини v утворюємо кліку для вершини v і її сусідів і виключаємо вершину, якщо залишаються ребра, інцидентні v але ще не покриті кліками[17].

• Двочасткова розмірність — найменше число біклік, необхідних для покриття ребер графу
• Задача про клікове покриття — NP-повна задача знаходження малої кількості клік, що покривають усі вершини графу

• Jonathan L. Gross, Jay Yellen. Graph Theory and its Applications. — CRC Press, 2006. — С. 440. — ISBN 978-1-58488-505-4.
• Fred S. Roberts. Applications of edge coverings by cliques // Discrete Applied Mathematics. — 1985. — Т. 10, вип. 1 (17 лютого). — С. 93—109. — DOI:10.1016/0166-218X(85)90061-7.
• E. Szpilrajn-Marczewski. Sur deux propriétés des classes d'ensembles // Fund. Math.. — 1945. — Т. 33 (17 лютого). — С. 303—307.
• Paul Erdős, A. W. Goodman, Lajos Pósa. The representation of a graph by set intersections // Canadian Journal of Mathematics. — 1966. — Т. 18, вип. 1 (17 лютого). — DOI:10.4153/CJM-1966-014-3.
• T. S. Michael, Thomas Quint. Sphericity, cubicity, and edge clique covers of graphs // Discrete Applied Mathematics. — 2006. — Т. 154, вип. 8 (17 лютого). — DOI:10.1016/j.dam.2006.01.004.
• V. K. Balakrishnan. Schaum's outline of theory and problems of graph theory. — McGraw-Hill Professional, 1997. — ISBN 978-0-07-005489-9.
• László Lovász. Proceedings of the Colloquium held at Tihany, Hungary, 1966 / P. Erdős, G. Katona. — Academic Press, 1968. Как цитировано у Робертса (Roberts, (1985))
• Noga Alon. Covering graphs by the minimum number of equivalence relations // Combinatorica. — 1986. — Т. 6, вип. 3 (17 лютого). — DOI:10.1007/bf02579381.
• J. B. Orlin. Contentment in graph theory: covering graphs with cliques // Proc. Kon. Ned. Acad. Wet.. — 1977. — Т. 80 (17 лютого). — С. 406—424. — DOI:10.1016/1385-7258(77)90055-5. Як процитиовано в Робертса (Roberts, (1985))
• L. T. Kou, L. J. Stockmeyer, C. K. Wong. Covering edges by cliques with regard to keyword conflicts and intersection graphs // Communications of the ACM. — 1978. — Т. 21, вип. 2 (17 лютого). — DOI:10.1145/359340.359346.
• Jens Gramm, Jiong Guo, Falk Hüffner, Rolf Niedermeier. Data reduction and exact algorithms for clique cover // Journal of Experimental Algorithmics. — 2009. — Т. 13, вип. 2 (17 лютого). — DOI:10.1145/1412228.1412236.
• Marek Cygan, Stefan Kratsch, Marcin Pilipczuk, Michał Pilipczuk, Magnus Wahlström. Automata, Languages, and Programming: 39th International Colloquium, ICALP 2012, Warwick, UK, July 9-13, 2012, Proceedings, Part I / Artur Czumaj, Kurt Mehlhorn, Andrew Pitt, Roger Wattenhofer. — 2012. — Т. 7391. — (Lecture Notes in Computer Science) — ISBN 978-3-642-31593-0. — DOI:10.1007/978-3-642-31594-7_22.
• Marek Cygan, Marcin Pilipczuk, Michał Pilipczuk. Proc. 24th ACM-SIAM Symposium on Discrete Algorithms (SODA 2013). — 2013.
• R. J. Opsut, F. S. Roberts. The Theory and Applications of Graphs / G. Chartrand, Y. Alavi, D. L. Goldsmith, L. Lesniak-Foster, D. R. Lick. — New York : Wiley, 1981. Як процитиовано в Робертса (Roberts, (1985))
• Edward R. Scheinerman, Ann N. Trenk. On the fractional intersection number of a graph // Graphs and Combinatorics. — 1999. — Т. 15, вип. 3 (17 лютого). — DOI:10.1007/s003730050068.
• М. Гэри, Д. Джонсон. Вычислительные машины и труднорешаемые задачи. — М. : «Мир», 1982.

• Weisstein, Eric W. Число перетинів(англ.) на сайті Wolfram MathWorld.