Граф перетинів
В теорії графів графом перетинів називається граф, що подає схему перетинів сімейства множин. Будь-який граф можна подати як граф перетинів, але деякі важливі спеціальні класи можна визначити за допомогою типів множин, що використовуються для подання у вигляді перетинів множин.
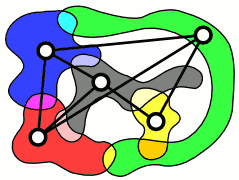
Огляд теорії графів перетинів і важливих спеціальних класів графів перетинів наведено в книзі Маккі і Макморріса[1].
Формальне визначення
Граф перетинів — це неорієнтований граф, утворений з сімейства множин
створенням вершини для кожної множини і з'єднанням двох вершин і ребром, якщо відповідні дві множини мають непорожній переріз, тобто
- .
Всі графи є графами перетинів
Будь-який неорієнтований граф G можна подати як граф перетинів — для будь-якої вершини графу G утворимо множину , що складається з ребер, інцидентних . Дві таких множини мають непорожній переріз тоді і лише тоді, коли відповідні вершини належать одному ребру. Ердеш, Ґудмен і Поза[2] показали більш ефективну побудову (яка вимагає менше елементів у всіх множинах ), в якій загальна кількість елементів у множинах не перевершує , де n — число вершин у графі. За їх твердженням, виявленням, що всі графи є графами перетинів, вони завдячують Марчевському[3], але також згадують і роботи Чулика[4]. Число перетинів графу — це мінімальне число елементів у поданнях графу, як графу перетинів.
Класи графів перетинів
Багато важливих сімейств графів можна описати як графи перетинів обмежених типів множин, наприклад, множин, отриманих з деяких геометричних конфігурацій:
- Інтервальний граф визначається як граф перетинів інтервалів на прямій, або зв'язних підграфів — шляхів.
- Граф дуг кола визначається як граф перетинів дуг кола.
- Коловий граф визначається як граф перетинів множини хорд кола.
- Граф багатокутників на колі визначається як граф перетинів багатокутників з вершинами, що лежать на колі.
- Одна з характеристик хордальних графів — це те, що вони є графами перетинів зв'язних підграфів дерева.
- Трапецеїдальний граф визначається як граф перетинів трапецій, утворених двома паралельними прямими. Він є узагальненням поняття графу перестановки, який, у свою чергу, є окремим випадком сімейства доповнень графів порівнянності, відомих як графи копорівнянності.
- Граф одиничних кіл визначається як граф перетинів одиничних кіл на площині.
- Теорема про пакування кіл стверджує, що планарні графи — це точно графи перетинів сімейств замкнутих дисків на площині, що не перетинаються (дозволено дотик).
- Гіпотеза Шайнермана (тепер — теорема) стверджує, що будь-який планарний граф можна подати у вигляді графу перетинів відрізків на площині. Однак графи перетинів відрізків на прямій можуть бути непланарними, і розпізнавання графів перетинів відрізків на прямій є повним для теорії існування дійсних чисел [5] .
- Реберний граф графу G визначається як граф перетинів ребер графу G, де кожне ребро розглядається як множина з двох його кінцевих вершин.
- Струнний граф — це граф перетинів кривих на площині.
- Граф має рамковість k, якщо він є графом перетинів багатовимірних прямокутників розмірності k, але не менших розмірностей.
Варіації та узагальнення
- Теоретичними аналогами порядку графів перетинів є порядки вкладеності . Точно так само, як подання графу перетинів позначає кожну вершину множиною інцидентних їй ребер, що мають непорожній перетин, подання порядку вкладеності f частково впорядкованої множини позначає кожен елемент такою множиною, що для будь-якого x і y в ній тоді і тільки тоді, коли.
Див. також
Примітки
Література
- K. Čulík. Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963). — Prague : Publ. House Czechoslovak Acad. Sci, 1964. — С. 13—20.
- Paul Erdős, A. W. Goodman, Louis Pósa. The representation of a graph by set intersections // Canadian Journal of Mathematics. — 1966. — Т. 18, вип. 1 (3 березня). — С. 106—112. — DOI:. — MR0186575.
- Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs. — Academic Press, 1980. — ISBN 0-12-289260-7.
- Topics in Intersection Graph Theory. — Philadelphia : Society for Industrial and Applied Mathematics, 1999. — Т. 2. — (SIAM Monographs on Discrete Mathematics and Applications) — ISBN 0-89871-430-3.
- E. Szpilrajn-Marczewski. Sur deux propriétés des classes d'ensembles // Fund. Math.. — 1945. — Т. 33 (3 березня). — С. 303—307. — MR0015448.
- Marcus Schaefer. Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers. — Springer-Verlag, 2010. — Т. 5849. — С. 334—344. — (Lecture Notes in Computer Science) — ISBN 978-3-642-11804-3. — DOI:
Посилання
- Jan Kratochvíl, A video lecture on intersection graphs (June 2007)
- E. Prisner, A Journey through Intersection Graph County
