Інтервальний граф
Інтервальний граф — граф перетинів мультимножини інтервалів на прямій. Має по одній вершині для кожного інтервалу в множині і по ребру між кожною парою вершин, якщо відповідні інтервали перетинаються.
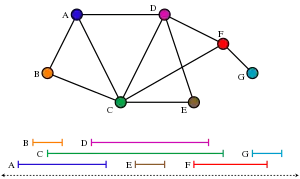
Визначення
Нехай — множина інтервалів.
Відповідний інтервальний граф — це G= (V, E), де
- і
- тоді і тільки тоді, коли .
Із цієї побудови можна отримати загальні властивості інтервальних графів. Так, граф G є інтервальним тоді і тільки тоді, коли найбільші кліки графу G можуть бути впорядковані так, що для будь-якого , де , виконується також для будь-якого [1].
Ефективні алгоритми розпізнавання
Визначити, чи є граф інтервальним можна за час шляхом впорядкування найбільших клік графу G.
Початковий алгоритм розпізнавання за лінійний час Бута і Люкера(Booth, Lueker, 1976) ґрунтується на складній структурі PQ-дерев, але Хабіб, МакКонел, Пауль і В'єно(Habib, McConnell, Paul, Viennot, 2000) показали, як розв'язати задачу простіше, використовуючи лексикографічний пошук у ширину і ґрунтуючись на факті, що граф є інтервальним тоді і тільки тоді, коли він хордальний і його доповнення — граф порівняння[1][2].
Пов'язані сім'ї графів
Інтервальні графи є хордальними, і, як наслідок, досконалими[1][2]. Їх доповнення належать до класу графів порівняння[3], і відношення порівняння — це інтервальний порядок[1].
Інтервальні графи, які мають інтервальне представлення, в якому будь-які два інтервали або не перетинаються, або вкладені, є тривіальними досконалими графами.
Правильні інтервальні графи — це інтервальні графи, які мають інтервальне представлення, в якому жоден інтервал не є власною підмножиною жодного іншого інтервалу. Одиничні інтервальні графи — це інтервальні графи, які мають інтервальне представлення, в якому кожен інтервал має одиничну довжину. Будь-який правильний інтервальний граф не має клешень. Але обернене твердження не є правильним — граф без клешень не обов'язково є правильним інтервальним графом[4]. Якщо набір сегментів є множиною, тобто повторення сегментів не є дозволеним, то граф є одиничним інтервальним графом тоді і тільки тоді, коли він є правильним інтервальним графом[5].
Графи перетинів дуг кола утворюють графи дуг кола — клас графів, який містить інтервальні графи. Трапецеїдальні графи, перетин трапецій, всі паралельні сторони яких лежать на двох паралельних прямих, є узагальненням інтервальних графів.
Шляхова ширина інтервального графу на одиницю менша, ніж розмір максимальної кліки (або, що є еквівалентним, на одиницю менша, ніж його хроматичне число), а шляхова ширина будь-якого графу G дорівнює найменшій шляховій ширині інтервального графу, який містить G як підграф.
Споріднені інтервальні графи без трикутників — це те ж, що і гусеничне дерево[6].
Застосування
Математичну теорію інтервальних графів створено з урахуванням застосувань дослідниками з математичного відділу корпорації RAND, в яку входили такі молоді дослідники, як Пітер Фішберн, студенти Алан Такер і Джоел Коуен, а також лідери, такі як Делберт Рей Фалкерсон і (частий гість) Віктор Клі[7]. Коуен застосував інтервальні графи у математичних моделях популяцій, особливо харчових ланцюгів[8].
Інші застосування включають генетику, біоінформатику та інформатику. Пошук множини відрізків, які представляють інтервальний граф, може використовуватися як методика збірки неперервних послідовностей в ДНК[9]. Інтервальні графи використовуються в підстановці задач на розміщення ресурсів, у дослідженнях операцій і плануванні виконання задач. Кожний відрізок представляє запит на ресурс на певний період часу. Задача знаходження незалежної множини максимальної ваги графу представляє задачу пошуку кращої підмножини запитів, які можна виконати без конфліктів[10].
Примітки
Література
- Amotz Bar-Noy, Reuven Bar-Yehuda, Ari Freund, Joseph (Seffi) Naor, Baruch Schieber. A unified approach to approximating resource allocation and scheduling // Journal of the ACM. — 2001. — Т. 48, вип. 5. — С. 1069—1090. — DOI:.
- Hans L. Bodlaender. A partial k-arboretum of graphs with bounded treewidth // Theoretical Computer Science. — 1998. — Т. 209, вип. 1—2. — С. 1—45. — DOI:.
- K. S. Booth, G. S. Lueker. Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms // J. Comput. System Sci. — 1976. — Т. 13, вип. 3. — С. 335—379. — DOI:.
- Joel E. Cohen (1978). Food webs and niche space. Monographs in Population Biology 11. Princeton, NJ: Princeton University Press. с. xv+1–190. ISBN 978-0-691-08202-8.
- Eckhoff. Extremal interval graphs // Journal of Graph Theory. — 1993. — Т. 17, вип. 1. — С. 117—127. — DOI:.
- Ralph Faudree, Evelyne Flandrin, Zdeněk Ryjáček. Claw-free graphs — A survey // Discrete Mathematics. — 1997. — Т. 164, вип. 1—3. — С. 87—147. — DOI:.
- Peter C. Fishburn. Interval orders and interval graphs: A study of partially ordered sets. — New York, 1985. — (Wiley-Interscience Series in Discrete Mathematics)
- D. R. Fulkerson, O. A. Gross. Incidence matrices and interval graphs // Pacific Journal of Mathematics. — 1965. — Т. 15. — С. 835—855.
- P. C. Gilmore, A. J. Hoffman. A characterization of comparability graphs and of interval graphs // Can. J. Math. — 1964. — Т. 16. — С. 539—548. — DOI:..
- Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs // Academic Press. — 1980. — ISBN 0-12-289260-7.
- Martin Charles Golumbic, Ron Shamir. Complexity and algorithms for reasoning about time: a graph-theoretic approach // J. Assoc. Comput. Mach. — 1993. — Т. 40. — С. 1108—1133..
- Michel Habib, Ross McConnell, Christophe Paul, Laurent Viennot. Lex-BFS and partition refinement, with applications to transitive orientation, interval graph recognition, and consecutive ones testing // Theor. Comput. Sci.. — 2000. — Т. 234. — С. 59—84. — DOI:.
- F.S. Roberts. Proof Techniques in Graph Theory. — Academic Press, New York. — 1969. — С. 139—146.
- Peisen Zhang, Eric A. Schon, Stuart G. Fischer, Eftihia Cayanis, Janie Weiss, Susan Kistler, Philip E. Bourne. An algorithm based on graph theory for the assembly of contigs in physical mapping of DNA // Bioinformatics. — 1994. — Т. 10, вип. 3. — С. 309—317. — DOI:.
Посилання
- interval graph. Information System on Graph Classes and their Inclusions.
- Weisstein, Eric W. {{{title}}}(англ.) на сайті Wolfram MathWorld.
