Число розв'язування
Число розв'язування в теорії вузлів — один з важливих інваріантів вузла, найменше число перемикання мостів, тобто число переходів крізь себе, після чого вузол розв'язується.
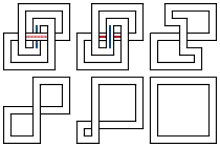
Трилисник розв'язується шляхом перемикання одного моста.
Числа розв'язування деяких вузлів
Будь-який складений вузол має число розв'язування щонайменше 2, а тому будь-який вузол з числом розв'язування 1 є простим. У таблиці наведено перші декілька вузлів та їхні числа розв'язування:
 Трилисник
Трилисник
число розв'язування = 1 Вісімка
Вісімка
число розв'язування = 1 Перстач
Перстач
число розв'язування = 2 Вузол на три півоберти
Вузол на три півоберти
число розв'язування = 1 Стивідорний вузол
Стивідорний вузол
число розв'язування = 1 6₂
6₂
число розв'язування = 1 6₃
6₃
число розв'язування = 1 7₁
7₁
число розв'язування = 3
Властивості
Якщо вузол має число розв'язування , існує діаграма вузла, яку можна звести до тривіального вузла перемиканням перетинів[1]. Число розв'язування вузла завжди менше від половини його числа перетинів[2].
У загальному випадку досить складно визначити число розв'язування заданого вузла. Випадки, для яких число розв'язування відоме:
- Число розв'язування нетривіального скрученого вузла завжди дорівнює 1.
- Число розв'язування -торичного вузла дорівнює .
- Числа розв'язування простих вузлів з числом перетинів дев'ять і менше відомі[3] (число розв'язування простого вузла 1011 невідоме).
Інші числові інваріанти вузлів
Див. також
Примітки
- Adams, 2004, с. 56.
- Taniyama, 2009, с. 1049—1063.
- Weisstein, Eric W. Unknotting Number(англ.) на сайті Wolfram MathWorld.
Література
- Kouki Taniyama. Unknotting numbers of diagrams of a given nontrivial knot are unbounded // Journal of Knot Theory and its Ramifications. — 2009. — Т. 18, вип. 8. — DOI:10.1142/S0218216509007361.
- Colin Conrad Adams. The knot book: an elementary introduction to the mathematical theory of knots. — Providence, Rhode Island : American Mathematical Society, 2004. — ISBN 0-8218-3678-1.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.