IDEA (шифр)

IDEA (англ. International Data Encryption Algorithm, міжнародний алгоритм шифрування даних) — симетричний блоковий алгоритм шифрування даних, запатентований швейцарською фірмою Ascom. Відомий тим, що застосовувався в пакеті програм шифрування PGP. У листопаді 2000 року IDEA був представлений як кандидат у проекті NESSIE в рамках програми Європейської комісії IST (англ. Information Societes Technology, інформаційні громадські технології).

Алгоритм блокового шифрування

Назва:	IDEA
Розробник:	Швейцарська фірма Ascom
Створений:	1991 р.
Опублікований:	1991 р.
Розмір ключа:	128 біт
Розмір блоку:	64 біт
Число раундів:	8,5
Тип:	модифікована мережа Фейстеля

Історія

Першу версію алгоритму розробили в 1990році Лай Сюецзя (Xuejia Lai) і Джеймс Мессі (James Massey) зі Швейцарського інституту ETH Zürich (за контрактом з Hasler Foundation, яка пізніше влилася в Ascom-Tech AG) як заміна DES (англ. Data Encryption Standard, стандарт шифрування даних) і назвали її PES (англ. Proposed Encryption Standard, запропонований стандарт шифрування). Потім, після публікації робіт Біхамом і Шаміра по диференціальному криптоанализу PES, алгоритм був поліпшений з метою посилення криптостійкості і названий IPES (англ. Improved Proposed Encryption Standard, покращений запропонований стандарт шифрування). Через рік його перейменували в IDEA (англ. International Data Encryption Algorythm).

Опис

Так як IDEA використовує 128-бітний ключ і 64-бітний розмір блоку, відкритий текст розбивається на блоки по 64 біт. Якщо таке розбиття неможливо, останній блок доповнюється різними способами певною послідовністю біт. Для уникнення витоку інформації про кожному окремому блоці використовуються різні режими шифрування. Кожен вихідний незашифрований 64 — біт ний блок ділиться на чотири підблока по 16 біт кожен, так як всі алгебраїчні операції, що використовуються в процесі шифрування, відбуваються над 16-бітними числами. Для шифрування і розшифрування IDEA використовує один і той же алгоритм.

Позначення операцій
⊞	Додавання по модулю $216$
⊙	Множення по модулю $216 +1$
⊕	Побітова виключна диз'юнкція

Фундаментальним нововведенням в алгоритмі є використання операцій з різних алгебраїчних груп, а саме:

Додавання по модулю $2^{16}$
Множення по модулю $2^{16}+1$
Побітова виключна диз'юнкція (XOR).

Ці три операції несумісні в тому сенсі, що ніякі дві з них не задовольняють дистрибутивному закону, тобто $a\odot (b\oplus c)\ \neq \ (a\odot b)\oplus (a\odot c)$ Застосування цих трьох операцій ускладнює криптоаналіз IDEA в порівнянні з DES, який базується виключно на операції виключає АБО, а також дозволяє відмовитися від використання S-блоків і таблиць заміни. IDEA є модифікацією мережі Фейстеля.

Генерація ключів

З 128-бітного ключа для кожного з восьми раундів шифрування генерується по шість 16-бітних подключів, а для вихідного перетворення генерується чотири 16-бітних підключа. Всього буде потрібно 52 = 8 x 6 + 4 різних подключів по 16 біт кожен. Процес генерації п'ятдесяти двох 16-бітних ключів полягає в наступному:

Насамперед, 128-бітний ключ розбивається на вісім 16-бітних блоків. Це будуть перші вісім подключів по 16 біт кожен — $(K_{1}^{(1)}K_{2}^{(1)}K_{3}^{(1)}K_{4}^{(1)}K_{5}^{(1)}K_{6}^{(1)}K_{1}^{(2)}K_{2}^{(2)})$
Потім цей 128-бітний ключ циклічно зсувається вліво на 25 позицій, після чого новий 128-бітний блок знову розбивається на вісім 16-бітних блоків. Це вже наступні вісім подключів по 16 біт кожен — $(K_{3}^{(2)}K_{4}^{(2)}K_{5}^{(2)}K_{6}^{(2)}K_{1}^{(3)}K_{2}^{(3)}K_{3}^{(3)}K_{4}^{(3)})$
Процедура циклічного зсуву і розбивки на блоки триває до тих пір, поки не будуть згенеровані всі 52 16-бітних підключа.

Таблиця підключів для кожного раунду
Номер раунду	Підключі
1	$K_{1}^{(1)}K_{2}^{(1)}K_{3}^{(1)}K_{4}^{(1)}K_{5}^{(1)}K_{6}^{(1)}$
2	$K_{1}^{(2)}K_{2}^{(2)}K_{3}^{(2)}K_{4}^{(2)}K_{5}^{(2)}K_{6}^{(2)}$
3	$K_{1}^{(3)}K_{2}^{(3)}K_{3}^{(3)}K_{4}^{(3)}K_{5}^{(3)}K_{6}^{(3)}$
4	$K_{1}^{(4)}K_{2}^{(4)}K_{3}^{(4)}K_{4}^{(4)}K_{5}^{(4)}K_{6}^{(4)}$
5	$K_{1}^{(5)}K_{2}^{(5)}K_{3}^{(5)}K_{4}^{(5)}K_{5}^{(5)}K_{6}^{(5)}$
6	$K_{1}^{(6)}K_{2}^{(6)}K_{3}^{(6)}K_{4}^{(6)}K_{5}^{(6)}K_{6}^{(6)}$
7	$K_{1}^{(7)}K_{2}^{(7)}K_{3}^{(7)}K_{4}^{(7)}K_{5}^{(7)}K_{6}^{(7)}$
8	$K_{1}^{(8)}K_{2}^{(8)}K_{3}^{(8)}K_{4}^{(8)}K_{5}^{(8)}K_{6}^{(8)}$
Вихідне перетворення	$K_{1}^{(9)}K_{2}^{(9)}K_{3}^{(9)}K_{4}^{(9)}$

Шифрування

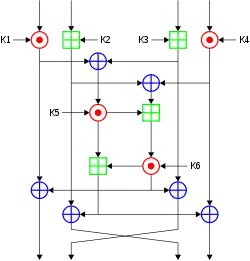
Структура алгоритму IDEA показана на малюнку. Процес шифрування складається з восьми однакових раундів шифрування і одного вихідного перетворення. Вихідний незашифрований текст ділиться на блоки по 64 біта. Кожен такий блок ділиться на чотири підблока по 16 біт кожен. На малюнку ці підблоки позначені $D_{1}$ , $D_{2}$ , $D_{3}$ , $D_{4}$ . У кожному раунді використовуються свої підключі згідно з таблицею підключів. Над 16-бітними підключами і підблока незашифрованого тексту проводяться наступні операції:

Множення по модулю $2^{16}+1$ = 65537, причому замість нуля використовується $2^{16}$
Додавання по модулю $2^{16}$
Побітове виключне АБО

В кінці кожного раунду шифрування є чотири 16-бітних підблоки, які потім використовуються як вхідні підблоки для наступного раунду шифрування. Вихідна перетворення являє собою скорочений раунд, а саме, чотири 16-бітних підблоки на виході восьмого раунду і чотири відповідних підключа піддаються операціям:

Множення по модулю $2^{16}+1$
Додавання по модулю $2^{16}$

Після виконання вихідного перетворення конкатенація підблоків $D_{1}'$ , $D_{2}'$ , $D_{3}'$ і $D_{4}'$ являє собою зашифрований текст. Потім береться наступний 64-бітний блок незашифрованого тексту і алгоритм шифрування повторюється. Так продовжується до тих пір, поки не зашифрують всі 64-бітові блоки вихідного тексту.

Математичний опис

Блок відкритого тексту розміром 64 біт ділиться на чотири рівні подблока розміром по 16 біт $(D_{1}^{(0)},D_{2}^{(0)},D_{3}^{(0)},D_{4}^{(0)})$
Для кожного раунду $(i=1...8)$ обчислюються:

A^{(i)}\ =\ D_{1}^{(i-1)}*K_{1}^{(i)}

B^{(i)}\ =\ D_{2}^{(i-1)}+K_{2}^{(i)}

C^{(i)}\ =\ D_{3}^{(i-1)}+K_{3}^{(i)}

D^{(i)}\ =\ D_{4}^{(i-1)}*K_{4}^{(i)}

E^{(i)}\ =\ A^{(i)}\oplus C^{(i)}

F^{(i)}\ =\ B^{(i)}\oplus D^{(i)}

D_{1}^{(i)}\ =\ A^{(i)}\oplus ((F^{(i)}+E^{(i)}*K_{5}^{(i)})*K_{6}^{(i)})

D_{2}^{(i)}\ =\ C^{(i)}\oplus ((F^{(i)}+E^{(i)}*K_{5}^{(i)})*K_{6}^{(i)})

D_{3}^{(i)}\ =\ B^{(i)}\oplus (E^{(i)}*K_{5}^{(i)}+(F^{(i)}+E^{(i)}*K_{5}^{(i)})*K_{6}^{(i)})

D_{4}^{(i)}\ =\ D^{(i)}\oplus (E^{(i)}*K_{5}^{(i)}+(F^{(i)}+E^{(i)}*K_{5}^{(i)})*K_{6}^{(i)})

Результатом виконання восьми раундів будуть наступні чотири подблока $(D_{1}^{(8)},D_{2}^{(8)},D_{3}^{(8)},D_{4}^{(8)})$

Виконується вихідне перетворення $(i=9)$ :

D_{1}^{(9)}\ =\ D_{1}^{(8)}*K_{1}^{(9)}

D_{2}^{(9)}\ =\ D_{3}^{(8)}+K_{2}^{(9)}

D_{3}^{(9)}\ =\ D_{2}^{(8)}+K_{3}^{(9)}

D_{4}^{(9)}\ =\ D_{4}^{(8)}*K_{4}^{(9)}

Результатом виконання вихідного перетворення є зашифрований текст $(D_{1}^{(9)},D_{2}^{(9)},D_{3}^{(9)},D_{4}^{(9)})$

Розшифрування

Метод обчислення, що використовується для розшифровки тексту по суті такий же, як і при його шифруванні. Єдина відмінність полягає в тому, що для розшифровки використовуються інші підключі. У процесі розшифровки підключі повинні використовуватися у зворотному порядку. Перший і четвертий підключі i-го раунду розшифровки виходять з першого і четвертого підключа (10-i)-го раунду шифрування мультиплікативною інверсією. Для 1-го та 9-го раундів другий і третій підключи розшифровки виходять з другого і третього подключів 9-го і 1-го раундів шифрування аддитивною інверсією. Для раундів з 2-го по 8-й другий і третій підключі розшифровки виходять з третього і другого подключів з 8-го по 2-й раундів шифрування аддитивною інверсією. Останні два підключа i-го раунду розшифровки рівні останніх двох підключів (9-i)-го раунду шифрування. Мультиплікативна інверсія підключа K позначається 1 / K і $(1/K)*K=1\mod \ (2^{16}+1)$ . Так як $2^{16}+1$ — просте число, кожне ціле не дорівнює нулю K має унікальну мультипликативну інверсію по модулю $2^{16}+1$ . Адитивна інверсія підключа K позначається-K і $-K+K=0\mod \ (2^{16})$ .

Таблиця підключів для кожного раунду
Номер раунду	Підключі
1	$1/K_{1}^{(9)}\ -K_{2}^{(9)}\ -K_{3}^{(9)}\ 1/K_{4}^{(9)}\ K_{5}^{(8)}\ K_{6}^{(8)}$
2	$1/K_{1}^{(8)}\ -K_{3}^{(8)}\ -K_{2}^{(8)}\ 1/K_{4}^{(8)}\ K_{5}^{(7)}\ K_{6}^{(7)}$
3	$1/K_{1}^{(7)}\ -K_{3}^{(7)}\ -K_{2}^{(7)}\ 1/K_{4}^{(7)}\ K_{5}^{(6)}\ K_{6}^{(6)}$
4	$1/K_{1}^{(6)}\ -K_{3}^{(6)}\ -K_{2}^{(6)}\ 1/K_{4}^{(6)}\ K_{5}^{(5)}\ K_{6}^{(5)}$
5	$1/K_{1}^{(5)}\ -K_{3}^{(5)}\ -K_{2}^{(5)}\ 1/K_{4}^{(5)}\ K_{5}^{(4)}\ K_{6}^{(4)}$
6	$1/K_{1}^{(4)}\ -K_{3}^{(4)}\ -K_{2}^{(4)}\ 1/K_{4}^{(4)}\ K_{5}^{(3)}\ K_{6}^{(3)}$
7	$1/K_{1}^{(3)}\ -K_{3}^{(3)}\ -K_{2}^{(3)}\ 1/K_{4}^{(3)}\ K_{5}^{(2)}\ K_{6}^{(2)}$
8	$1/K_{1}^{(2)}\ -K_{3}^{(2)}\ -K_{2}^{(2)}\ 1/K_{4}^{(2)}\ K_{5}^{(1)}\ K_{6}^{(1)}$
Вихідне перетворення	$1/K_{1}^{(1)}\ -K_{2}^{(1)}\ -K_{3}^{(1)}\ 1/K_{4}^{(1)}$

Приклад

Для зручності числа представляємо в шістнадцятковому вигляді.

Приклад шифрування

Як 128-бітний ключ використовуємо K = (0001,0002,0003,0004,0005,0006,0007,0008), а як 64-бітний відкритий текст M = (0000,0001, 0002,0003)

Таблиця підключів і підблоків для кожного раунду
Раунд	Раундові ключі						Значення блоків даних
Раунд	$K_{1}^{(i)}$	$K_{2}^{(i)}$	$K_{3}^{(i)}$	$K_{4}^{(i)}$	$K_{5}^{(i)}$	$K_{6}^{(i)}$	$D_{1}^{(i)}$	$D_{2}^{(i)}$	$D_{3}^{(i)}$	$D_{4}^{(i)}$
—	—	—	—	—	—	-	0000	0001	0002	0003
1	0001	0002	0003	0004	0005	0006	00f0	00f5	010a	0105
2	0007	0008	0400	0600	0800	0a00	222f	21b5	f45e	e959
3	0c00	0e00	1000	0200	0010	0014	0f86	39be	8ee8	1173
4	0018	001c	0020	0004	0008	000c	57df	ac58	c65b	ba4d
5	2800	3000	3800	4000	0800	1000	8e81	ba9c	f77f	3a4a
6	1800	2000	0070	0080	0010	0020	6942	9409	e21b	1c64
7	0030	0040	0050	0060	0000	2000	99d0	c7f6	5331	620e
8	4000	6000	8000	a000	c000	e001	0a24	0098	ec6b	4925
9	0080	00c0	0100	0140	-	-	11fb	ed2b	0198	6de5

Приклад розшифровки

Як 128-бітного ключа використовуємо K = (0001,0002,0003,0004,0005,0006,0007,0008), а як 64-бітного зашифрованого тексту C = (11fb, ed2b, 0198,6 de5)

Таблиця підключів та підблоків для кожного раунду
Раунд	Раундові ключі						Значення блоків даних
Раунд	$K_{1}^{'(i)}$	$K_{2}^{'(i)}$	$K_{3}^{'(i)}$	$K_{4}^{'(i)}$	$K_{5}^{'(i)}$	$K_{6}^{'(i)}$	$D_{1}^{(i)}$	$D_{2}^{(i)}$	$D_{3}^{(i)}$	$D_{4}^{(i)}$
1	fe01	ff40	ff00	659a	c000	e001	d98d	d331	27f6	82b8
2	fffd	8000	a000	cccc	0000	2000	bc4d	e26b	9449	a576
3	a556	ffb0	ffc0	52ab	0010	0020	0aa4	f7ef	da9c	24e3
4	554b	ff90	e000	fe01	0800	1000	ca46	fe5b	dc58	116d
5	332d	c800	d000	fffd	0008	000c	748f	8f08	39da	45cc
6	4aab	ffe0	ffe4	c001	0010	0014	3266	045e	2fb5	b02e
7	aa96	f000	f200	ff81	0800	0a00	0690	050a	00fd	1dfa
8	4925	fc00	fff8	552b	0005	0006	0000	0005	0003	000c
9	0001	fffe	fffd	c001	-	-	0000	0001	0002	0003

Апаратна реалізація

Апаратна реалізація має такі переваги:

Істотне підвищення швидкості шифрування за рахунок використання паралелізму при виконанні операцій
Менше енергоспоживання

Перша реалізація алгоритму IDEA на інтегральній схемі (англ. Very Large Scale Integration) була розроблена і верифікована Лаем, Мессі і Мерфі в 1992 рік у з використанням технологічного процесу 1,5 мкм і технології КМОН Швидкість шифрування даного пристрою становила 44 Мб / сек.

В 1994 рік у Карігером, Бонненбергом, Зіммерманом та ін було розроблено пристрій VINCI. Швидкість шифрування даної реалізації IDEA становила 177 Мб / сек при тактовій частоті 25 МГц, техпроцес 1,2 мкм. Це було перше напівпровідниковий пристрій, який вже могло застосовуватися для шифрування в реальному часі в таких високошвидкісних мережних протоколах, як ATM (англ. Asynchronous Transfer Mode, асинхронний режим передавання) або FDDI (англ. Fiber Distributed Data Interface, розподілений волоконний інтерфейс даних). Швидкість 177 Мб / сек була досягнута завдяки використанню досить витонченої схеми конвеєрної обробки і чотирьох звичайних помножувачів по модулю $2^{16}+1$ . У пристрої також використовуються два односпрямованих високошвидкісних 16-бітних порту даних. Ці порти забезпечують постійну завантаженість блоків шифрування.

Криптостійкість

Алгоритм IDEA з'явився в результаті незначних модифікацій алгоритму PES. На малюнку наведено структури обох алгоритмів, і видно, що змін не так вже й багато:

Множення підблока $D_{2}$ з другим підключимо раунду замінено складанням
Складання підблока $D_{4}$ з четвертим підключимо раунду замінено на множення
Змінений зрушення^[Що?] підблоків в кінці раунду

Один з найбільш відомих у світі криптологів Брюс Шнаєр у своїй книзі «Прикладна криптографія» зауважив: «… дивно, як такі незначні зміни можуть привести до настільки великим відмінностей».

У тій же книзі, що вийшла в 1996 року, Брюс Шнаєр відгукнувся про IDEA так: «Мені здається, це найкращий і надійний блоковий алгоритм, опублікований дотепер».

В алгоритмі IDEA використовує 64-бітові блоки. Довжина блоку повинна бути достатньою, щоб приховати статистичні характеристики вихідного повідомлення. Але зі збільшенням розміру блоку експоненціально зростає складність реалізації криптографічного алгоритму. В алгоритмі IDEA використовується 128-бітний ключ. Довжина ключа повинна бути досить великою, щоб запобігти можливості перебору ключа. Для розкриття 128-бітного ключа повним перебором ключів за умови, що відомий відкритий і відповідний йому зашифрований текст, потрібно $2^{128}$ (порядку $10^{38}$ ) шифрування . При такій довжині ключа IDEA вважається досить безпечним. Висока крипостійкість IDEA забезпечується також такими характеристиками:

Заплутування — шифрування залежить від ключа складним і заплутаним чином
Розсіювання — кожен біт незашифрованого тексту впливає на кожен біт зашифрованого тексту

Лай Сюецзя (Xuejia Lai) і Джеймс Мессі (James Massey) провели ретельний аналіз IDEA з метою з'ясування його криптостійкості до диференціальному криптоаналізу . Для цього ними було введено поняття марківського шифру і продемонстровано, що стійкість до диференціального криптоаналізу може бути промодельована і оцінена кількісно. Лінійних або алгебраїчних слабкостей у IDEA виявлено не було. Спроба взлому за допомогою криптоаналізу з пов'язаними ключами, проведена Біхамом (Biham), також не увінчалася успіхом[1].

Існують успішні атаки, що застосовуються до IDEA з меншим числом раундів (повний IDEA має 8.5 раундів). Успішною вважається атака, якщо взлом шифру з її допомогою вимагає меншої кількості операцій, ніж при повному переборі ключів. Метод розкриття Віллі Майера (Willi Meier) виявився ефективніше взлому повним перебором ключів тільки для IDEA з 2 раундами

Методом «зустріч посередині» був взломаний IDEA з 4,5 раундами. Для цього потрібне знання всіх $2^{64}$ блоків відкритих текстів і складність аналізу становить $2^{112}$ операцій. Найкраща атака на 2007 рік застосовна до всіх ключам і може зламати IDEA з 6-ма раундами.

Слабкі ключі

Існують великі класи слабких ключів. Слабкі вони в тому сенсі, що існують процедури, що дозволяють визначити, чи відноситься ключ до даного класу, а потім і сам ключ. В даний час відомі наступні:

$2^{23}+2^{35}+2^{51}$ слабких до диференціальному криптоаналізу ключів. Приналежність до класу $2^{51}$ можна обчислити за $2^{12}$ операцій за допомогою підібраного відкритого тексту. Автори даної атаки запропонували модифікацію алгоритму IDEA. Дана модифікація полягає в заміні підключів $K_{i}^{(r)}$ на відповідні $K_{i}^{'(r)}\ =a\oplus K_{i}^{(r)}$ , де r — номер раунду шифрування. Точне значення a не критично. Наприклад при $a\ =\ 0dae$ (в шістнадцятковій системі числення) дані слабкі ключі виключаються.

$2^{63}$ слабких до лінійного диференціального криптоаналізу ключів. Приналежність до даного класу з'ясовується за допомогою тесту на пов'язаних ключах.

$2^{53}+2^{56}+2^{64}$ слабких ключів було знайдено з використанням методу бумеранга (англ. boomerang attack), запропонованого Девідом Вагнером ( David Wagner). Тест на приналежність до даного класу виконується за $2^{16}$ операцій і потребують $2^{16}$ елементів пам'яті.

Існування таких великих класів слабких ключів не впливає на практичну крипостійкість алгоритму IDEA, тому що повна множина всіх можливих ключів становить $2^{128}$ .

Примітки

E. Biham, personal communication, 1993

Література

Gulom Numovych Tuychiev. Алгоритми шифрування ГОСТ 28147-89-IDEA8-4 и ГОСТ 28147-89-RFWKIDEA8-4 // Захист інформації. — НАУ, 2017. — Т. 19. — ISSN 2410-7840. — DOI:10.18372/2410-7840.19.11199.

Посилання

RSA FAQ on Block Ciphers (англійською). Архів оригіналу за 19 жовтня 2004. Процитовано 6 ноября 2008.
SCAN entry for IDEA (англійською). Архів оригіналу за 28 січня 2012. Процитовано 6 ноября 2008.
IDEA Applet (німецькою). Архів оригіналу за 1 лютого 2012. Процитовано 6 ноября 2008.
Erläuterung und Schaubild zum Verfahren (німецькою). Архів оригіналу за 28 січня 2012. Процитовано 6 ноября 2008.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] E. Biham, personal communication, 1993